矩阵的特征值【相关词_ 矩阵的特征值怎么求】

其中A和B为矩阵。其广义特征值(第二种意义)λ可以通过求解方程(A-λB)ν=0,得到det(A-λB)=0(其中det即行列式)构成形如A-λB的矩阵的集合。其中特征值中存在的复数项

设α0是A属于特征值λ0的特征向量,则α0不一

623x456 - 24KB - JPEG

2016考研数学:计算数字矩阵特征值的三个技巧

598x720 - 77KB - JPEG

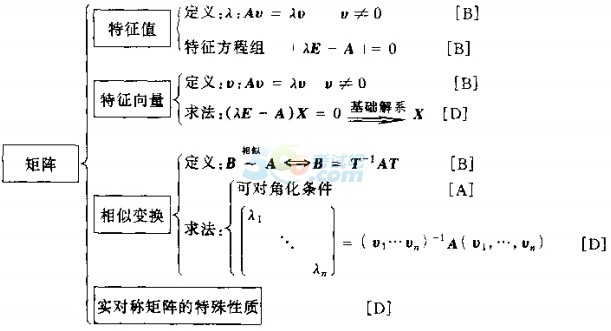
2015考研数学知识框架图:矩阵特征值和特征向

611x331 - 38KB - JPEG

矩阵的逆的特征值和原矩阵的特征值的关系是什

648x486 - 120KB - JPEG

矩阵的特征值怎么球_矩阵的乘法_钟爱阁 -

391x220 - 6KB - JPEG

矩阵的特征值怎么球_矩阵的乘法_钟爱阁 -

293x220 - 4KB - JPEG

【线性代数】矩阵的特征值与特征向量

826x500 - 52KB - JPEG

矩阵和行列式的区别_矩阵的特征值_钟爱阁 -

287x220 - 8KB - JPEG

如何直观理解矩阵的特征值和特征向量_鹿

690x435 - 36KB - JPEG

MATLAB矩阵特征值画图 - MATLAB 基础讨论

447x336 - 30KB - JPEG

2017考研线性代数公式大全:矩阵的特征值和特

465x599 - 54KB - JPEG

2016考研数学:矩阵乘积的特征值剖析

585x323 - 49KB - JPEG

第5.1节 矩阵的特征值与特征向量(吕)PPT_wor

1080x810 - 73KB - JPEG

views计算矩阵特征值_如何计算矩阵的特征值_

398x238 - 15KB - JPEG

矩阵特征值的理论及应用.pdf

703x1026 - 208KB - PNG