 抽象函数
抽象函数
500x375 - 11KB - JPEG
 高考专题:抽象函数
高考专题:抽象函数
215x155 - 3KB - JPEG
 抽象函数定义域,初学= =,理解不能.已知f(x)
抽象函数定义域,初学= =,理解不能.已知f(x)
1350x742 - 79KB - JPEG
 复习专题5--抽象函数的奇偶性周期性对称性
复习专题5--抽象函数的奇偶性周期性对称性
993x1404 - 95KB - PNG
抽象函数
752x499 - 35KB - PNG
 抽象函数专题
抽象函数专题
1982x2809 - 9KB - PNG
 抽象函数专题
抽象函数专题
1982x2809 - 6KB - PNG
 用周期性求抽象函数值的方法
用周期性求抽象函数值的方法
725x453 - 57KB - PNG
 高中数学抽象函数专题
高中数学抽象函数专题
649x455 - 39KB - JPEG
 抽象函数与初等函数的微妙解法
抽象函数与初等函数的微妙解法
1518x918 - 662KB - PNG
 抽象函数
抽象函数
635x498 - 32KB - JPEG
 抽象函数习题精选精讲
抽象函数习题精选精讲
1188x1684 - 546KB - PNG
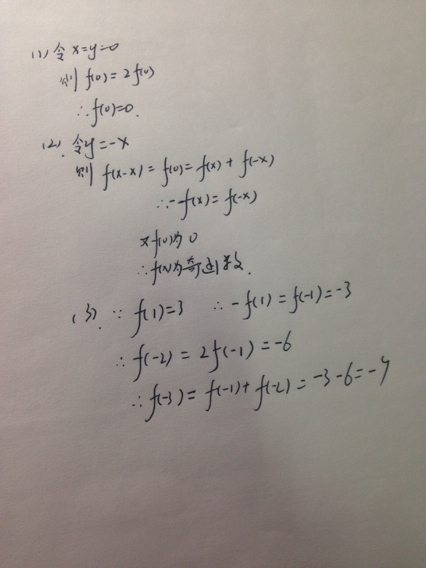 抽象函数
抽象函数
426x568 - 195KB - JPEG
 高考专题; 抽象函数1
高考专题; 抽象函数1
649x402 - 32KB - JPEG
 抽象函数
抽象函数
1075x717 - 107KB - JPEG
简介:我们把没有给出具体解析式的函数称为抽象函数。由于这类问题可以全面考查学生对函数概念和性质的理解,同
抽象函数专题讲座抽象函数是指没有明确给出具体的函数表达式,只是给出一些特殊条件的函数。一.抽象函数定义域1.已知的定义域,求的定义域其解法是:若的定义域为,则在中,,从中解得的取值范围即为的定义域.例1.已知函数的定义域为,求的定义域.解:的定义域为,,.故函数的定义域为.2、已知的定义域,求的
高考抽象函数技巧总结由于函数概念比较抽象,学生对解有关函数记号的问题感到困难,学好这部分知识,能加深学生对函数概念的理解,更好地掌握函数的性质,培养灵活性;提高解题能力,优化学生数学思维素质。现将常见解法及意义总结如下:一、求表达式:1.换元法:即用中间变量表示原自变量的代数式,从而
抽象函数解题方法与技巧函数的周期性:1、定义在x∈R上的函数y=f(x),满足f(x+a)=f(x-a)(或f(x-2a)=f(x))(a>0)恒成立,则y=f(x)是周期为2a的周期函数;2、若y=f(x)的图像关于直线x=a和x=b对称,则函数y=f(x)是周期为2|a-b|的周期函数;3、若y=f(x) 的图像关于点(a,0)和(b,0)对称,则函数y=f(x)是周期为2|a-b|的周期函数;4、若y=f(x) 的图像
简介 本课程将抽象函数和具体的函数模型对应结合,以帮助大家理解、攻克函数中这类比较难理解的问题。 贝婕数学系列课程力求将高考考点一网打尽。使认真学完全套课程
[最佳答案] 令x=1 y=1 f(1*1)=f(1)+f(1) f(1)=o 令x=-1 y=-1 f(-1*(-1))=f(-1)+f(-1)=0 2f(-1)=0 f(-1)=0 令y=-1 f(-x)=f(-1*x)=f(-1)+f(x)=f(x) 所以是偶函数 令y=1/x f(x*1/x)=f(x)+f(1/x)=f(1)=0 那么f(1/x)=-f(x) 如果x1<x2 f(1/x1)=-f(x1) f(x2*1&
[最佳答案] 向左转|向右转
郑重声明:本文内容由学而思培优提供,版权归高考网所有,禁止转载。考点提示:抽象函数相关问题,要学会基本的赋值,如加法为核心的关系式中赋0,相