余弦定理证明_余弦定理的证明方法

余弦定理证明相关问答

余弦定理的八种证明方法研究背景:2011年高考数学卷(陕西卷)考出了“说明并证明余弦定理”这个考题,使平时不注重翻阅课本的同学大部分吃了亏,虽然这是书本上的知识,且课本上只给出了一种证明方法,但仍让同学们很难想到会考这个证明题,因此我们利用这次研究性学习活动,以论文的方式来介绍一下多

1.三角形基本公式:(1)内角和定理:A+B+C=180°,sin(A+B)=sinC, cos(A+B)= -cosC,cos=sin, sin=cos(2)面积公式:S=absinC=bcsinA=casinBS= pr = (其中p=, r为内切圆半径)(3)射影定理:a = bcosC + ccosB;b = acosC + ccosA;c = acosB + bcosA2.正弦定理: 证明:由三角形面积得画出三角形的外接圆及直径易得: 3.余弦定理:a2=b2+c2-2bccosA,; 证明:如图ΔABC中,当A、B

若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。下面是高三网小编整理的余弦定理多种证明方法,希望对高中生的数学学习

简介：余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理。运用它可解决一类已知三角形两边及夹角

[最佳答案] 在△abc中，ab＝c、bc＝a、ca＝b 则c^2＝a^2＋b^2－2ab*cosc a^2＝b^2＋c^2－2bc*cosa b^2＝a^2＋c^2－2ac*cosb 下面在锐角△中证明第一个等式，在钝角△中证明以此类推。 过a作ad⊥bc于d ，则bd＋cd＝a 由勾股定理得： c^2＝(ad)^2＋(bd)^2 ，(ad)^2＝b^2－(cd)^2 所以c^2＝(ad)^2－(cd)^2＋b^2 ＝(a－cd)^2－(cd

doc格式-9页-文件0.02M-余弦定理证明过程(精选多篇)余弦定理证明过程(精选多篇)余弦定理证明过程 ma=?(c +(a/2) -ac*cosb) =(1/2)?(4c +a -4ac*cosb)由b =a +c -2ac*cosb得

余弦定理的十一种证明方法余弦定理和勾股定理一样,证明方法也有很多种,下面给出比较经典的十一种证明方法,供大家参考!余弦定理:三角形任一边的平方等于另外两边的平方和减去这两边与其夹角余弦的积的二倍。如图1所示,在△ABC中,若AB=c,BC=a,CA=b,则有:c2=a2+b2-2abcosCa2=b2+c2-2bccosAb2=c2+a2-2cacosB.【证法1】如

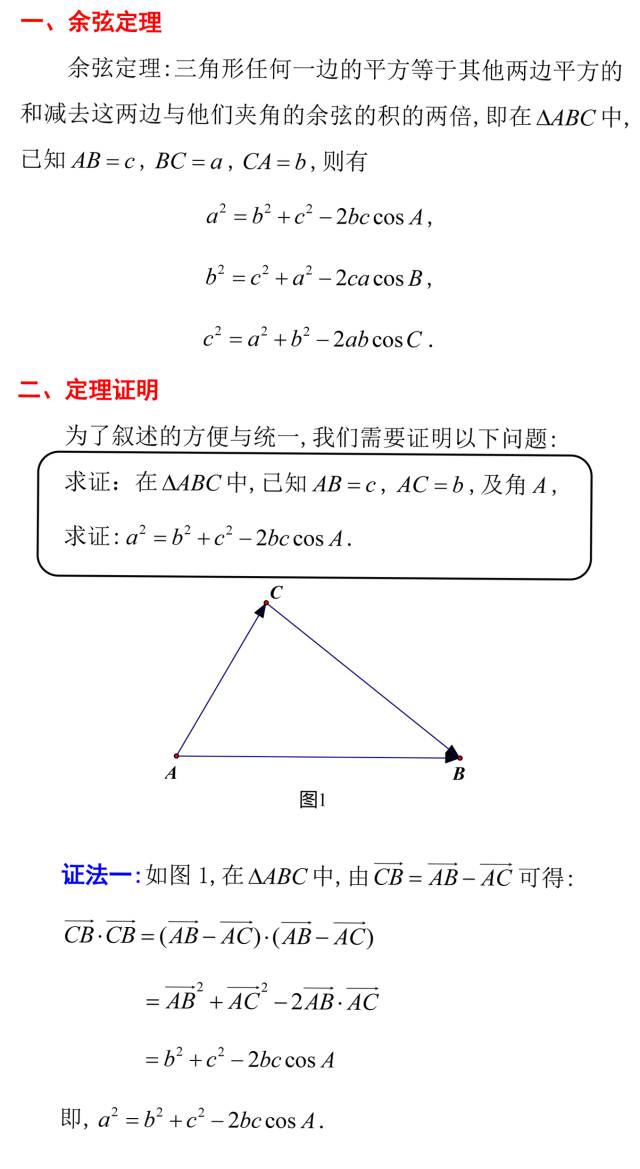
(经典)最全余弦定理的10种证明方法--王彦文 青铜峡一中一、余弦定理余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的积的两倍,即在中,已知, , ,则有,,.二、定理证明为了叙述的方便与统一,我们证明以下问题即可:在中,已知, ,及角,求证:.证法一:如图1,在中,由可得:即,.

请叙述并证明余弦定理?

答：余弦定理:三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍;或在△ABC中,a,b,c为A,B,C的对边,有a2=b2+c2-2bccosA,b2=c2+a2-2cacosB

余弦定理的证明

答： a^2=b^2+c^2-2bc*cosA b^2=a^2+c^2-2ac*cosB 下面在锐角△中证明第一个等式,在钝角△中证明以此类推。 过A作AD⊥BC于D ,则BD+CD=a 由勾股定理得: c^2=(AD

余弦定理怎么证明?

答：/2ac CosA=(c^2+b^2-a^2)/2bc 证明: 如图: ∵a=b-c ∴a^2=(b-c)^2 (证明中前面所写 b^2=c^2+a^2-2ac*cosB cosB=(c^2+a^2-b^2)/2ac 从余弦定理和余弦函数的性质可以看

余弦定理的证明!??

答：证明: 如图: ∵a=b-c ∴a^2=(b-c)^2 (证明中前面所写的a,b,c皆为向量,^2为平方)拆开 ∠A所对的边为a 则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c 根据勾股定理可

正弦定理和余弦定理证明

答： 因为在同圆或等圆中同弧所对的圆周角相等,所以∠D等于∠ACB.  所以c/sinC=c/sinD=BD=2R  类似可证其余两个等式。余弦定理的证明:在任意△ABC中  做

证明:余弦定理

答：/2ac CosA=(c^2+b^2-a^2)/2bc 证明: 如图: ∵a=b-c ∴a^2=(b-c)^2 (证明中前面所 所对的角是锐角.即,利用余弦定理,可以判断三角形形状。 同时,还可以用余弦定理求三

用余弦定理证明:在三角形ABC中,当∠C为锐角时,a?+b?>c?;当

答：运用余弦定理证明这道题是最简单的方法。余弦定理如下:c?=a?+b?-2abCosC∵在三角形ABC中,0°<∠C<180°且cosC在[0,π]上单调递减当C∈[0,π/2]时,cosC>0;当C∈(π

正弦定理和余弦定理的证明

答：正弦定理 证明 步骤1 在锐角△ABC中,设BC=a,AC=b,AB=c。作CH⊥AB垂足为点H 所以∠D等于∠C. 所以c/sinC=c/sinD=BD=2R 类似可证其余两个等式。 余弦定理

用余弦定理证明 平行四边形两条对角线平方和等于四边平方的

答： AC^2=a^2+b^2-2abcosB BD^2=a^2+b^2-2abcos(180°-B)=a^2+b^2+2abcosB 两式相加, AC^2+BD^2=a^2+b^2+a^2+b^2,得证。