 12-5全微分方程PPT
12-5全微分方程PPT
1080x810 - 171KB - JPEG
 大一高数,全微分方程,画波浪线的两行,上
大一高数,全微分方程,画波浪线的两行,上
644x457 - 132KB - JPEG
 DA12_5全微分方程PPT
DA12_5全微分方程PPT
1080x810 - 97KB - JPEG
 高等数学 第十二章 微分方 第五节 全微分方程
高等数学 第十二章 微分方 第五节 全微分方程
1077x805 - 78KB - JPEG
 常微分方程23全微分方程
常微分方程23全微分方程
1080x810 - 118KB - JPEG
 2020山东专升本考试:全微分方程
2020山东专升本考试:全微分方程
678x352 - 77KB - PNG
 全微分方程1PPT
全微分方程1PPT
1080x810 - 86KB - JPEG
 12-5全微分方程
12-5全微分方程
1080x810 - 171KB - JPEG
 【求助】一道 全微分方程
【求助】一道 全微分方程
600x480 - 61KB - JPEG
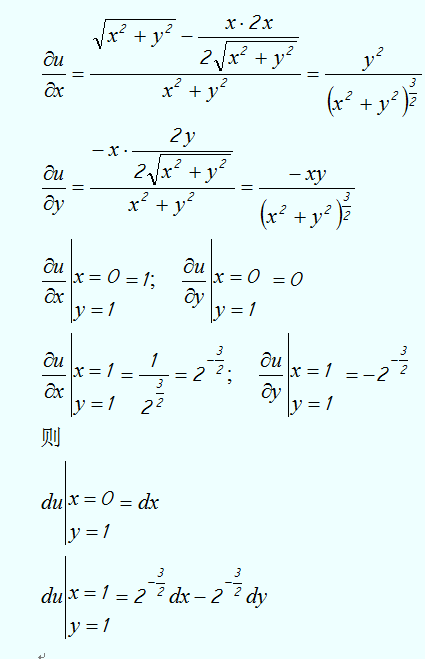 方程在点的全微分
方程在点的全微分
425x659 - 7KB - PNG
高等数学全微分方程.
1080x810 - 80KB - JPEG
 全微分方程PPT
全微分方程PPT
1080x810 - 86KB - JPEG
 12全微分方程PPT
12全微分方程PPT
1080x810 - 94KB - JPEG
 全微分方程
全微分方程
620x377 - 91KB - JPEG
7-5 全微分方程
1080x810 - 127KB - JPEG
简介:的全微分,即 dU(x,y)=P(x,y)dx+Q(x,y)dy则称Pdx+Qdy=0为全微分方程或恰当微分方程,显然,这时该方程的通解为U(x
全微分方程的解法 VIP专享文档 VIP专享文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买VIP专享文档下载特权礼包的其他会员用户可用VIP专享文档下载特
[最佳答案] 若p(x,y)dx+q(x,y)dy=du(x,y),则称pdx+qdy=0为全微分方程,显然,这时该方程通解为u(x,y)=c(c是任意常数). 方程中的未知数含有微分的情况,只要有dx 对于未知数x 这就是个全微分方程
全微分方程 VIP专享文档 VIP专享文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买VIP专享文档下载特权礼包的其他会员用户可用VIP专享文档下载特权免费
[最佳答案] 若P(x,y)dx+Q(x,y)dy=du(x,y),则称Pdx+Qdy=0为全微分方程,显然,这时该方程通解为u(x,y)=C(C是任意常数). 方程中的未知数含有微分的情况,只要有dx 对于未知数x 这就是个全微分方程
是全微分方程,则称$μ(x,y)$为方程的积分因子 定理1:$μ(x,y)$是方程积分因子的充要条件是$$\frac{∂(μM)}{∂y}=\frac{∂(μM)}{∂x}$$ 定理2:若$μ(x,y)$是方程的一个积分因子
详细讲解了全微分方程的概念,性质,与连续,偏导数的关系,及计算方法,对大学高数学习及考研复习都有很大帮助。 VIP专享文档 VIP专享文档是百度文库认证用户/机构上传的专
[最佳答案] 不可能对,您的理解有问题,没明白全微分方程的实质。全微分方程实际上是方程可以写成d(f(x,y))=0的形式,然后对两边同时取积分,解得f(x,y)=C为原方程的解,例如2xdx=-3y^2 方程可以化为d(x^2)+d(y^3)=0等价于d(x^2+y^3)=0直接积分得x^2+y^3=c,因此原方程也可以直接积分。 你自己设出来y=-4这样一个初始条件解出来的夜是原方程的解,但是很遗憾解出来的是某一个奇解或者奇解上的某一个点,如果方程要求你解通解的话那肯定不对。 从这个题目来看是考察积分因子的,如果是高数里的题目那直接分离变量积分然后化成那种形式即可,如果是数学院或者工学院的常微分方程课程的内容的话,你翻开全微分方程和积分因子这一节,先套公式求出来积分因子把方程化为全微分方程再解。