 快速傅里叶变换原理附其应用.doc
快速傅里叶变换原理附其应用.doc
793x1122 - 41KB - PNG
 快速傅里叶变换的原理与方法.pdf全文-综合
快速傅里叶变换的原理与方法.pdf全文-综合
800x1221 - 222KB - PNG
 快速傅里叶变换基2时间抽取FFT算法
快速傅里叶变换基2时间抽取FFT算法
529x348 - 87KB - PNG
 快速傅里叶变换(FFT)算法--理论与程序设计
快速傅里叶变换(FFT)算法--理论与程序设计
870x1229 - 91KB - PNG
 基于LabVIEW的平均FFT(快速傅立叶)变换_
基于LabVIEW的平均FFT(快速傅立叶)变换_
893x579 - 97KB - PNG
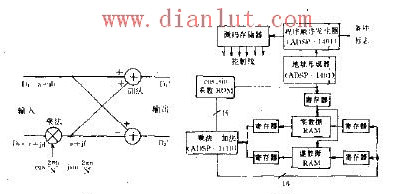 【图】快速傅里叶变换算法FFT运算器电路
【图】快速傅里叶变换算法FFT运算器电路
411x194 - 39KB - JPEG
 快速傅里叶变换简介_什么是快速傅里叶
快速傅里叶变换简介_什么是快速傅里叶
200x122 - 6KB - JPEG
 第五章 离散傅里叶变换及其快速算法
第五章 离散傅里叶变换及其快速算法
459x265 - 16KB - JPEG
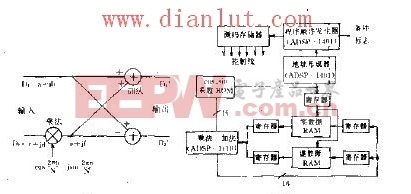 快速傅里叶变换算法FFT运算器电路图
快速傅里叶变换算法FFT运算器电路图
411x194 - 60KB - JPEG
 快速傅里叶变换简介_什么是快速傅里叶
快速傅里叶变换简介_什么是快速傅里叶
200x98 - 5KB - JPEG
 按频率抽取基2-快速傅里叶逆变换算法_
按频率抽取基2-快速傅里叶逆变换算法_
993x1404 - 79KB - PNG
 基于LabVIEW与离散傅里叶变换法的能谱
基于LabVIEW与离散傅里叶变换法的能谱
445x262 - 74KB - JPEG
快速傅里叶变换实验报告
955x421 - 27KB - PNG
 离散傅里叶变换及其快速算法PPT
离散傅里叶变换及其快速算法PPT
1080x810 - 58KB - JPEG
 快速傅立叶变换FFT频谱分析程序.doc
快速傅立叶变换FFT频谱分析程序.doc
993x1404 - 219KB - PNG
简介:快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统
FFT(Fast Fourier Transformation) 快速傅里叶变换 ,是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。 而
FFT有什么用快速傅里叶变换 (fast Fourier transform),即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT。快速傅里叶变换是1965年由J.W.库利和
快速傅里叶变换 我们前面提到过,一个$n$次多项式可以被$n$个点唯一确定。 那么我们可以把单位根的$0$到$n-1$次幂带入,这样也可以把这个多项式确定出来。但是这样仍然
快速傅里叶变换(Fast Fourier Transform,FFT)是一种可在 时间内完成的离散傅里叶变换(Discrete Fourier transform,DFT)算法。 在算法竞赛中
快速傅里叶变换FFT \(O(nlogn)\)计算离散傅里叶变换 使用分治的思想,按下标奇偶分类,\(A_0(x)\)是偶数项,\(A_1(x)\)是奇数项,则\(A(x)=A_0(x^2)+xA_1(x^2)\),根据折半引理仅有\(
[最佳答案] 离散傅立叶变换(DFT)的定义: 为了表达简洁,令,则。 FFT的种类很多,这里以最简单的基于2的FFT(信号长度是2的整数幂)为例: FFT实际上一种分治算法。FFT将长度为的信号分解成两个长度为信号进行处理,这样分解一直到最后,每一次的分解都会减少计算的次数。理解FFT分以下三个步骤进行: 步骤1:将信号分解成两个子信号 偶数样本点信号:; 奇数样本点信号:; 则: 步骤2:将两个求和项理解成两个长度为的DFT 其中,所以 其中,偶数样本点信号的DFT: 奇数样本点信号的DFT: 步骤3:FFT的具体计算过程(通过蝶形图可视化) 由于对和都具有周期性:,所以, ,(周期性) 以为例,信号的FFT计算过程如下: 第1次分解: 第2次分解: 第3次分解: FFT与DFT的性能比较 根据DFT的定义, 对于任意都要进行次加法操作,所以DFT共有次乘法操作。 对于任意都要进行次加法操作,所以DFT共有次加法操作。 从FFT的蝶形图中可以看出, 共有次乘法操作和次加法操作。
快速傅里叶变换(FFT)的原理及公式 点击文档标签,更多精品内容等你发现~ 知道了 百科大全才|2018-06-29 VIP专享文档 VIP专享文档是百度文库认证用户/机构上传的专业性文