 匈牙利算法示例PPT
匈牙利算法示例PPT
1080x810 - 23KB - JPEG
 《管理运筹学》分配问题与匈牙利算法
《管理运筹学》分配问题与匈牙利算法
1080x810 - 30KB - JPEG
匈牙利算法与分枝定界法解决调色问题之比较
1280x1869 - 531KB - PNG
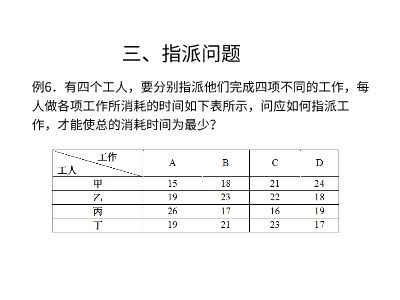 指派问题及匈牙利算法
指派问题及匈牙利算法
400x300 - 17KB - JPEG
 指派问题与匈牙利算法
指派问题与匈牙利算法
1080x810 - 143KB - JPEG
 匈牙利算法在企业员工指派问题的应用(
匈牙利算法在企业员工指派问题的应用(
439x397 - 165KB - PNG

851x306 - 100KB - PNG
 匈牙利算法和KM算法简介PPT
匈牙利算法和KM算法简介PPT
1080x810 - 101KB - JPEG
 匈牙利算法示例ppt
匈牙利算法示例ppt
1080x810 - 94KB - JPEG
 毕业设计与论文(匈牙利算法在企业员工
毕业设计与论文(匈牙利算法在企业员工
953x1333 - 322KB - PNG
 自动或立体仓库货位规划匈牙利算法堆垛机
自动或立体仓库货位规划匈牙利算法堆垛机
993x1404 - 62KB - PNG
 毕业设计与论文(匈牙利算法在企业员工
毕业设计与论文(匈牙利算法在企业员工
951x1331 - 136KB - PNG
 指派问题_匈牙利算法.ppt
指派问题_匈牙利算法.ppt
1152x864 - 187KB - PNG
 二分图最大婚配 - 匈牙利算法 - 综合
二分图最大婚配 - 匈牙利算法 - 综合
213x285 - 19KB - PNG
整数规划解法-匈牙利 算法部分
1080x810 - 34KB - JPEG
简介:匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想
本文讲述的是匈牙利算法,即图论中寻找最大匹配的算法,暂不考虑加权的最大匹配(用KM算法实现),文章整体结构如下:基础概念介绍算法的实现好的,开始!一.部分基础概念的介绍
可以看到,在上面的二分图中,每条边的端点都分别处于点集X和Y中。匈牙利算法主要用来解决两个问题:求二分图的最大匹配数和最小点覆盖数。 这么说起来过于抽象了,我们现
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,
由增广路的性质,增广路中的匹配边总是比未匹配边多一条,所以如果我们放弃一条增广路中的匹配边,选取未匹配边作为匹配边,则匹配的数量就会增加。匈牙利算法就是在不断
匈牙利算法的步骤:第一步 变换效率矩阵,使各行各列都出现 0 元素。1°效率矩阵每行元素都减去该行最小元素;2°效率矩阵每列元素都减去该列最小元素。第二步 圈出不同行且不同列的 0 元素,进行试指派。1°(行搜索)给只有一个0 元素的行中的0 画圈,记作“◎”,并划去与其同列的其余0元素;2°(列搜索)给只
高教研究·6·匈牙利算法及其在指派问题中的应用邓敏英阳彩霞胡学瑞武汉生物工程学院数学课部,湖北武汉431400摘要:本文主要论述了匈牙利算法的原理、步骤及其在指派
匈牙利算法的MATLAB 程序代码如下(算例):m=5;n=5;A=[0 1 1 0 01 1 0 1 10 1 1 0 00 1 1 0 00 0 0 1 1];M(m,n)=0;for(i=1:m)for(j=1:n)if(A(i,j))M(i,j)=1;break;end;end %求初始匹配Mif(M(i,j))break;end;end %获得仅含一条边的初始匹配Mwhile(1)for(i=1:m)x(i)=0;end %将记录X中点的标号和标记*for(i=1:n)y(i)=0;end %将记录Y中点的标号和标记*for(i=1:m)pd=1; %寻找X中