 为什么1\/sinx的不定积分不是-ln(cscx+cotx)_36
为什么1\/sinx的不定积分不是-ln(cscx+cotx)_36
450x800 - 43KB - JPEG
 文章- 积分公式
文章- 积分公式
110x200 - 5KB - JPEG
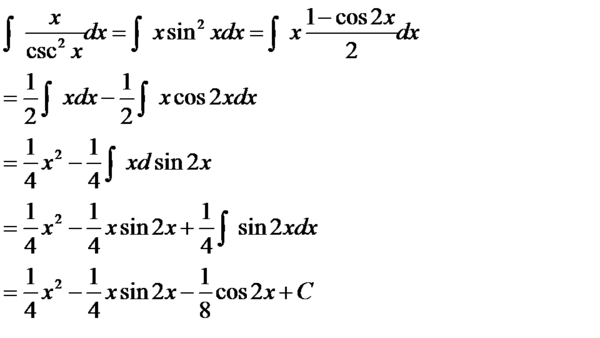 积分号x\/(cscx)的平方dx等于什么?
积分号x\/(cscx)的平方dx等于什么?
600x338 - 41KB - PNG
 【400+考研】公式大全(高数、线代、概率论应
【400+考研】公式大全(高数、线代、概率论应
800x1131 - 184KB - PNG
 IC型号74ABT541CSCX,【74ABT541八路缓冲
IC型号74ABT541CSCX,【74ABT541八路缓冲
850x1100 - 10KB - PNG
 74ABT273CSCX (FAIRCHILD) PDF技术资料下
74ABT273CSCX (FAIRCHILD) PDF技术资料下
850x1100 - 14KB - PNG
 38cscx
38cscx
380x277 - 26KB - JPEG
 74ABT374CSCX PDF资料下载(6\/6 页)High-S
74ABT374CSCX PDF资料下载(6\/6 页)High-S
816x1056 - 6KB - PNG
 IC型号74ABT541CSCX,【74ABT541八路缓冲
IC型号74ABT541CSCX,【74ABT541八路缓冲
850x1100 - 30KB - PNG
 74ABT374CSCX
74ABT374CSCX
816x1056 - 7KB - PNG
 74ABT125CSCX (ETC) PDF技术资料下载 74
74ABT125CSCX (ETC) PDF技术资料下载 74
850x1100 - 31KB - PNG
 74ABT374CSCX (FAIRCHILD) PDF技术资料下
74ABT374CSCX (FAIRCHILD) PDF技术资料下
300x388 - 44KB - PNG
 用 智能静音 恒温 水箱8年包换 JSQ26-CSCX(
用 智能静音 恒温 水箱8年包换 JSQ26-CSCX(
350x350 - 64KB - JPEG
 衫男士商务休闲职业工装衬衣白色40码CSCX0
衫男士商务休闲职业工装衬衣白色40码CSCX0
350x350 - 26KB - JPEG
 74ABT373CSCX PDF资料下载(3\/11 页)Micro
74ABT373CSCX PDF资料下载(3\/11 页)Micro
816x1056 - 4KB - PNG