借用协议_ PoD-Tiny——实现零信任交易的最简协议

摘要：zkPoD原理解读系列

本文作者：郭宇

本文面向有一定密码学基础，或者对密码学感兴趣的读者。文中虽有大量数学公式出现，但都比较简单不难理解。

导言：zkPoD是什么？

zkPoD实现了去中心化的「零知识有条件支付」，支持上GB数据的零信任公平交易。关于「零知识有条件支付」的概念请看这篇概述文章『zkPoD：区块链，零知识证明与形式化验证，实现无中介、零信任的公平交易』。zkPoD是一个全新的实现ZKCP目标的方案。目前zkPoD已经支持上GB的数据，支持低TPS公链，也支持高TPS联盟链；既支持二进制数据，也支持带有内部丰富类型与结构的表格数据。与传统的「受信第三方」相比，zkPoD利用区块链来作为一个「Trustless第三方」，实现「零信任公平交易」。

zkPoD也是一个实现数据与价值双向流通的底层基础协议

zkPoD开源代码与更多文档请见：https://github.com/sec-bit/zkPoD-node

Proof-ofDelivery协议

PoD是实现zkPoD系统的核心协议。PoD协议实现了借用区块链智能合约来进行「数据」和「Token」的原子交换，并且保证买卖双方的公平性。PoD并没有像ZKCP那样采用单一的zkSNARK方案来实现原子交换，而是利用了PedersenCommitment，SchnorrProtocol等密码学经典方案。这样PoD可以做得更高效，同时易扩展。PoD协议还将利用形式化的证明来构建坚实的「信任根基」。

本文介绍一个极简的PoD协议——PoD-Tiny，这个协议简化了很多细节，并不实用，但是可以帮助读者快速理解PoD的原理和面临的挑战。

假设我是卖家，而你需要从我手里买一个数据文件，这个协议的一个大致流程是：

步骤一：我把「数据」加密后，传给你步骤二：你把「Token」交给区块链「智能合约」步骤三：我用「密钥」交换「智能合约」手里的「Token」，然后你紧接着可以从智能合约中读取「密钥」进行「数据」解密是不是很简单？聪明的你此刻正在高度怀疑这个过程是不是哪有问题。

「公平交易」中的关键问题

关键问题：你收到的加密数据确实是你想要的数据关键问题：你收到加密数据之后，不付钱就跑路怎么办关键问题：而我出示给智能合约的密钥必须是真密钥，否则拿不到Token关键问题：我出示真密钥之后，必须要能拿到Token我们接下来就抽丝剥茧，讨论下PoD-Tiny是怎么巧妙解决这些问题的。

锁定数据的特征：Authenticator

对于关键问题，我们需要一个锚点，什么是你想要的数据。这里简单起见，假设我们事先约定了一个数据文件的唯一标签，或者特征。然后你购买的数据需要能和这个标签一一对应。

一般来说，大家喜欢用Hash来标记对一个字符串的特征，比如计算

h=MD5解决这个问题是核心方法是「零知识证明」。如果买家拿到加密数据之后，从中分析不出来任何多余的信息，那么就不会损害卖家利益，也就能解决关键问题。简单讲，如果加密数据是零知识的，就不怕买家拿了加密数据不给钱就跑路。所谓的「零知识」，大家可以这么通俗理解：买家拿到的加密数据后，就像拿到一堆随机数一样，没有任何信息量。怎么做到零知识呢？PoD-Tiny采用了经典Schnorr协议的思想。

关键问题：你收到加密数据之后，不付钱就跑路怎么办回忆一下关键问题：

通过同态性，买家可以在数据加密的情况验证数据是否满足一些条件

总结一下：

并且，通过上面的公式，你还能知道一个关键信息：密钥是一个关联到K的数值。尽管这时候你完全不知道m和密钥k。这个信息也是解决关键问题的关键所在。

E*G?=K+A

剩下的事情就简单了，在PoD协议中，我们可以任选一个随机数k作为一次性密钥，来加密m，计算E=k+m。E就是加密数据。我可以把K=k*G也发给你，这样你手里有三样东西，A，K，还有E。你就可以用下面的公式来「同态地」校验加了密的E确实是数据m的密文：

注：这里的加法是模加，a+b是a+bmodp的简写。为了易读性，后续的加减乘除一律约定是有限域上的运算。

来验证m1?=m2+m3。大家可以发现，虽然一个吃瓜群众知道了A1，他也不能反算出m1。但是他仍然知道m1等于另外两个数的和，虽然他完全不知道这三个数具体的值是多少。

我们可以计算A1?=A2+A3

A1=m1*G，A2=m2*G，A3=m3*G，

他们的Authenticator分别计算如下：

「认证信息」为什么要采用这种「承诺」形式，而不是采用大家所熟知的Hash运算。这是因为「承诺」具有加法运算同态性。所谓同态性质，大家可以这么理解：明文数据具有的某种运算，可以同态映射到密文的运算中。假设有三个数据明文，m1，m2还有m3，其中m1=m2+m3。

「认证信息」Authenticator可以向所有人公开，我们不用担心会泄露原始数据信息。这是因为，通过A难以反算出来m。这个逆运算是一个有限域的「求对数」运算。假如有限域比较大的话，这个对数运算是非常非常困难的，这就是常说的「离散对数难题」假设。抛开这些理论细节，我们只要知道，Authenticator可以放心交给任何人，而不用担心m被逆向破解。

承诺也叫Commitment，它可以做到和数据的一一对应，同时并且能够隐藏数据的值。这里的A在zkPoD系统中被称为「认证信息」Authenticator。而这里的G是一个椭圆曲线循环群的生成元。

A=m*G

我们通过下面的运算产生这个数据的「承诺」。

我们看下这个字符串"hello,zkPoD!"总共有12个字节大小，也就是96个bit。于是我们可以将这12个字节转换成一个有限域上的整数。这样我们可以把这个字符串编码成一个整数，我们姑且用一个符号表示这个整数，假设是m。

插播科普：Schnorr协议与「零知识」

Schnorr协议是非常经典的教课书例子，我这里快速带大家过一遍。Schnorr协议的用途之一是用来做身份认证，它是一个两方安全协议，一方「证明者」Alice，向另一方「验证者」Bob证明她拥有一个公钥对应的私钥。

首先Alice产生一对「公私钥」，。然后Bob持有Alice的公钥PK。当Alice要向Bob证明身份时，他们会通过一个「三步交互协议」来完成证明：证明Alice拥有私钥sk。如果Bob接受了这个证明，那么Bob会认为对面证明有私钥的人就是Alice。下面简单描述下这个协议：

sk=a,pk=a*G

公开输入：PK=a*G

Alice私有输入：sk=a

第一步：Alice选择一个随机数r，并且发送r的「承诺」R=r*G给Bob

第二步：Bob发回一个随机数c，作为挑战数

第三步：Alice计算z=r+c*a，然后将z发送给Bob，然后Bob通过如下的公式来验证：

验证公式：z*G?=R+c*PK=r*G+c*a*G

这个Schnorr协议具有三个性质：

完备性Completeness可靠性SpecialSoundness对诚实验证者零知SpecialHonestVerifierZero-Knowledge其中第三个性质就是「零知识」，这个性质保证了：在协议交互过程中，Bob无论如何都不会得到关于私钥的任何信息。

注:严格地讲，Schnorr协议并不是「Full-ZK」，只能保证「HVZK」，这是一个相对弱一些的零知识性质。不过大家暂时不用纠结这一点，Schnorr协议可以通过一些技巧升级为「Full-ZK」。

PoD-Tiny：一个简单的PoD协议

如果大家已经大概记住了Schnorr协议的细节，那么我来展示一个协议叫做PoD-Tiny。

协议描述：假设Alice拥有一个数据明文m，然后Bob拥有这个数据的Authenticator，这里还有一个「Trustless第三方」，我们暂且叫她Julia。请大家记住：她是一个智能合约。

协议：

开场前的道具：m,a,G,一个随机数产生器rand

角色：

Alice：拥有数据m，一次性密钥k<-randBob：拥有AJulia:N>

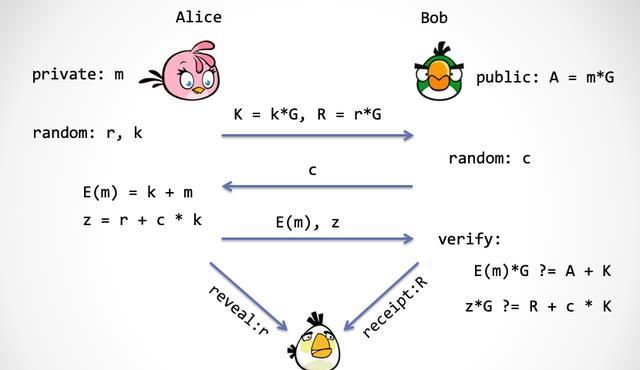
步骤：

第一步：Alice产生一个随机数，r<-rand，然后发给Bob两个数K=k*G和R=r*G<>

第二步：Bob产生一个随机数c<-rand，发送给Alice<>

第三步：Alice计算两个数字E=k+m，z=r+c*k，并且发送给Bob。这两个数，第一个E是用一次性密钥k加密后的「数据密文」，而z是「密钥的密文」。

注：什么？密钥的密文？没错，这里Alice用第一步生成的随机数r，加上第二步Bob提供的挑战数c对k做了加密，得到了z。

第四步：Bob对收到的数据密文E进行验证，并且对密钥的密文进行验证：

验证公式：E*G?=A+K验证公式：z*G?=R+c*K注：在第四步中，Bob需要搞明白两件事：首先传给他的密文数据能不能对应到数据锚点；然后密文数据是不是由某一个未知密钥X加密的，并且这个「未知密钥」的密文应该等于第三步中Alice发过来的「密钥密文」。倘若如此，在未来的某个时刻，若Bob得到「密钥密文的密钥」之后，就可以做两次解密动作来成功拿到数据明文。两次解密动作为：首先Bob用「密钥密文的密钥」r还有挑战数c解密密钥密文z，得到数据密钥k，然后再用数据密钥来解密数据密文E，从而得到数据明文m。再注：上面的协议第一步到第四步，其实大家可以发现和Schnorr协议非常类似。只不过把a替换成了一个一次性密钥k。然后另一个不同点是，K=k*G相当于原Schnorr协议中的公钥，并不是一开始发给了Bob，而是在协议的第一步和R一起发送给Bob。不管如何，从整体上，这四步协议正是一个Schnorr协议的扩展。当然到这里还没完，接下来区块链要登场了，Bob，Alice要和Julia开始进行交互。第五步：如果Bob在第四步中验证公式和公式通过，那么说明Alice发的加密数据都是正确的。这时候Bob要发给Julia一个「数据交付收据」，R。Bob在这一步需要将「Token」一并保存给Julia。

注：这个收据是为了告诉Julia，Bob他已经收到了加过密的数据了，但是密钥还没收到。密钥需要Julia帮他接收并验证。那么验证的凭据是什么呢？正是「密钥密文的密钥」对应的「承诺」，是不是有点绕，这个收据就是协议第一步Alice发给Bob的R。

第六步：Alice向Julia出示「密钥密文的密钥」，也就是r。Julia检查下面这个关键公式。如果验证通过，Julia可以将Bob保存的Token转给Alice。

验证公式：R?=r*G我们看看关键问题是如何解决的。关键问题：Alice出示给智能合约的密钥必须是真密钥，否则拿不到Token在协议的第一步，Alice给Bob发送了一个「密钥的密钥」的「承诺」R；然后在协议的第五步，Bob把R转交给了Julia；第六步，Alice兑现承诺，揭示对应的r。如果Alice出示一个错误的值，Julia立即就会发现公示不成立。还有一个：

关键问题：Alice出示真密钥之后，必须要能拿到Token在协议的第六步，Julia要检验公式。在Alice出示正确的r的情况下，如果等式不成立，那么只有两种情况：Julia故意捣乱，R的值不正确。对于前一种情况，需要保证Julia的合约代码确实没有漏洞，功能正常，这个需要额外采用「形式化验证」的方法来解决。对于后一种情况，这里需要Alice在第六步先检查一下Julia的内部状态，在第五步中Bob提交的R是不是一个正确的值。这里请注意：Julia是一个公开的智能合约，她持有的任何数据都是公开可见的，她的任何内部状态与计算过程都是公开可见的。

协议的安全性与公平性分析

如果我们不考虑多次交易，PoD-Tiny是一个「公平」的交易协议。我们接下来依次分析下为何这个协议是公平的。

我们首先考虑Alice有哪些作弊手段：

A1.将假的数据m'加密后传给BobA2.加密数据时用的密钥k，但是在加密密钥的时候却用的是另一个k'，并且k<>k'A3.向Julia出示一个假的密文密钥r'分析：如果Alice采用作弊手法A1，那么Bob在校验公式时能够发现；如果Alice采用作弊手法A2，那么Bob可以通过计算公式发现；如果Alice采用作弊手法A3，那么Julia通过公式能发现。

我们再考虑Bob都有哪些作弊手段：

B1.Bob在拿到加密数据E之后，就退出协议，然后尝试破解密文B2.Bob在验证加密数据之后，向Julia出示一个错误的「交付收据」B3.Bob账户没有足够的Token分析：如果Bob采用作弊手段B1，那么Bob是无法从加密数据中得到任何信息的，因为协议的前三步是「零知识的」。如果Bob采用手段B2，Alice可以在第六步检查下Julia手里的「数据交付收据」R是不是和她在第一步发给Bob的相同，一旦Bob提交错误的收据，Alice可以直接退出协议，拒绝出示密钥。同样，如果Bob采用手段B3，Alice可以在第六步的时候检查Bob保存在Julia处的Token是否足够，如果不足则直接退出协议。

最后，Julia有没有可能作弊呢？Julia是智能合约，她的任何行为和内部状态都能被任何人读取，那么通过Julia是有可能产生信息泄露的，从而对Alice或者Bob不利。但是请大家注意下，Julia其实并不接触任何和数据明文m相关的信息，也就从链上不会泄露m的信息。Julia接触到的信息只有两个，R和r。

压缩到最简协议

我们数一数上面的协议的交互步骤总共有五步，分别是Alice与Bob交互三次，Bob与Julia交互一次，Alice与Julia交互一次。安全协议里面有一个叫做Fiat-ShamirHeuristic变换的工具，它可以将PoD-Tiny协议中的前三次交互，直接「压缩」成为一次交互。

压缩前：

压缩后：

我们发现最主要的不同点是，在压缩后的PoD-Tiny中挑战数不再由Bob产生，而是由Alice产生。这里大家可能会产生疑问，这样做会不会对Bob不公平？这相当于三步的Schnorr协议直接压缩成一步就完成了。这里先下个结论：压缩后的协议保持零知识的性质，仍然对双方公平。原因是，压缩前的协议可以证明HVZK；压缩后的协议可以证明出NIZK。但是安全性在压缩前后的对比会比较Subtle，这里不再展开。

经过压缩，最后这个协议变得不可思议地简洁：

迈向实用性的挑战：安全与性能

最简协议PoD-Tiny只是万里长征的第一步，当面对纷繁冗杂的现实世界，要将理论变成代码时，会面临许许多多的问题。这些问题会相互纠缠在一起，反过来又会影响着协议在理论层面的设计。

如何支持长度超过1MB的数据，甚至上GB如何有效降低链上验证计算的开销如何支持以太坊，并免疫以太坊上的各式安全问题如何支持数据的复杂同态计算在安全和性能方面，zkPoD做了不少的工程改进和创新，感兴趣的朋友请