什么什么不什么_ 除了圆周率 你知道祖冲之还做了什么

圆周率是怎么计算出来的？我也一直曾是个疑问，在很久之前。在查了一些资料以后，崇敬变成了震惊，甚至是疑惑！！！

也许每一个中国人都不会不知道祖冲之，因为他的圆周率！当然，这不是他第一个发现的，但是他的确把圆周率计算到了一个极其精细的程度上了，精细到我们现在还在使用这个数字！在一千多年以前，怎么能不让人佩服得五体投地！所以，我是带着极为崇敬的心情写这些文字，不仅仅是因为他是我的老乡！

圆周率是怎么计算出来的？我也一直曾是个疑问，在很久之前。在查了一些资料以后，崇敬变成了震惊，甚至是疑惑！！！

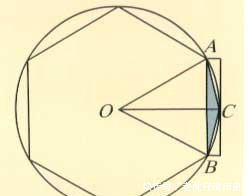
这大概是祖冲之甚至是祖冲之的前辈们运用的推理图的样式。用圆内接正多边形的周长来逼近圆周长，刘徽计算到圆内接96边形，求得π=3.14，并指出，内接正多边形的边数越多，所求得的π值越精确。这难道是微积分的起源么？

我几乎无法想想这个牛人是怎么计算的，当然祖冲之更牛！他把圆周率精确到小数点后面的七位数，我们当然知道每精确一位需要多大的计算量。没有任何的计算机！仅凭手工计算，这到底是怎么完成的！这当然是一个难题，难到直到将近1000年以后才被阿拉伯数学家卡西打破纪录。

然而，更牛的是，这不过是祖冲之众多贡献中的一个小部分。更厉害的是他还提出了球体的计算公式！这当然是比圆形面积的计算更难的一个成就！但这仍然是微不足道的，对这位数学天才！

我认为祖冲之最伟大的成就一是《缀术》，这也许是当时世界上最伟大的数学典籍，虽然他失传了！越是伟大的东西可能越是难以流传，这可能是世界历史上的一个怪现象！当然留下的一定是最实用的，比如说下面这两个：大明历和指南车！

凡事研究术数的人没有不知道大明历的，在祖冲之之前一直是19年七闰，祖冲之把它改为391年144闰。我们当然知道没一个月的时间并不是规则的30天，然而到底是多少时间，在当时当然是一个难题。《大明历》采用的朔望月长度为29.5309日，这和利用现代天文手段测得的朔望月长度相差不到一秒钟。这几乎是一个不可能的可能发生了！他是怎么计算的？这和上面说的那不什么小时的《缀术》有什么关系？当我们仰望星空的时候，便引起了无限的遐思！

在祖冲之之前！大家认为冬至的位置是不变的，然而事实总是和理论有了差距！这当然给生产生活带来了太多的困扰。农时那是一刻也差不得的啊！祖冲之的大明历引入了岁差的理念，巧妙的解决了这个问题，如果没有大明历，二十四节气的概念会不会被极为依赖农耕的中国古人所抛弃呢？也许我们都没有一个准确的答案！

另一个当然是指南车！“圆转不穷，而司方如一”（《南齐书·祖冲之传》）、“日行百余里”。在当时速度不谓不快啊！关键是一个新的机械化的时代似乎就要开始了，人类似乎就要打飞跃式的发展了......只是当时为啥也失传了！？