数学期望与方差的公式【相关词_数学期望公式方差公式】

期望与方差的相关公式 - 、数学期望的来由 早在 17 世纪, 有一个赌徒向法国著名数学家 方差的定义 前面我们介绍了随机变量的数学期望,它体现了随机变量取值的平均水平, 是

方差公式

300x239 - 8KB - JPEG

超几何分布列的数学期望和方差公式

463x273 - 17KB - JPEG

数学期望ex和方差dx_数学期望与方差公式_样

550x764 - 181KB - JPEG

统计学中常见的分布的数学期望和方差

567x313 - 14KB - PNG

[泊松分布的期望和方差]期望 方差公式的证明全

1048x786 - 107KB - JPEG

[泊松分布的期望和方差]期望 方差公式的证明全

1058x794 - 119KB - JPEG

[泊松分布的期望和方差]期望 方差公式的证明全

1048x786 - 95KB - JPEG

[泊松分布的期望和方差]期望 方差公式的证明全

1069x802 - 115KB - JPEG

020 Г函数在正态分布数学期望及方差公式推导

1786x2381 - 799KB - JPEG

020 Г函数在正态分布数学期望及方差公式推导

1786x2381 - 684KB - JPEG

数学二项式和超几何分布的方差公式推理 几何

500x742 - 74KB - JPEG

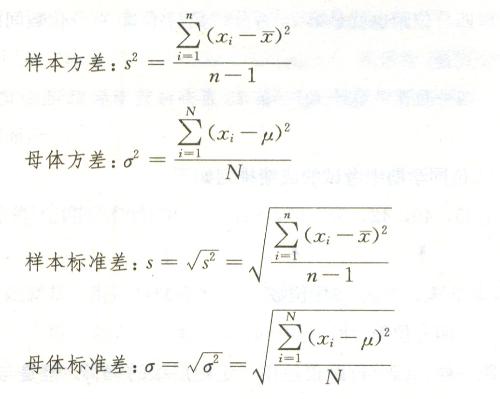
方差公式+-+搜搜百科

500x399 - 17KB - JPEG

已知随机变量X的数学期望E(X)与方差D(X)皆存

800x660 - 87KB - JPEG

2018考研数三公式大全(12):期望及方差公式-数

531x801 - 56KB - PNG

[泊松分布的期望和方差]期望 方差公式的证明全

1069x802 - 101KB - JPEG