函数求导相关图片
 基本初等函数求导公式与微分公式
基本初等函数求导公式与微分公式
642x987 - 69KB - JPEG
 初等函数求导PPT_word文档在线阅读与下载_无忧文档
初等函数求导PPT_word文档在线阅读与下载_无忧文档
1080x810 - 74KB - JPEG
 高等数学入门--反函数的求导法则(上)
高等数学入门--反函数的求导法则(上)
500x374 - 95KB - PNG
 复合函数求导公式
复合函数求导公式
586x426 - 35KB - PNG
 函数求导公式三角函数导数公式sec 请问三角函数怎么求导函数比如说y=cosx
函数求导公式三角函数导数公式sec 请问三角函数怎么求导函数比如说y=cosx
500x515 - 49KB - JPEG
 复合函数求导的一题:u=x-y,v=x+y,z=f(u,v) ez\/ex=ez\/eu+ez\/ev,两边对x求偏导数得(这步怎么算的) (看得清么)
复合函数求导的一题:u=x-y,v=x+y,z=f(u,v) ez\/ex=ez\/eu+ez\/ev,两边对x求偏导数得(这步怎么算的) (看得清么)
500x375 - 40KB - JPEG
 后高考时代1 基本初等函数求导公式推导2
后高考时代1 基本初等函数求导公式推导2
2883x4051 - 1086KB - JPEG
 幂函数求导公式
幂函数求导公式
993x1404 - 55KB - PNG
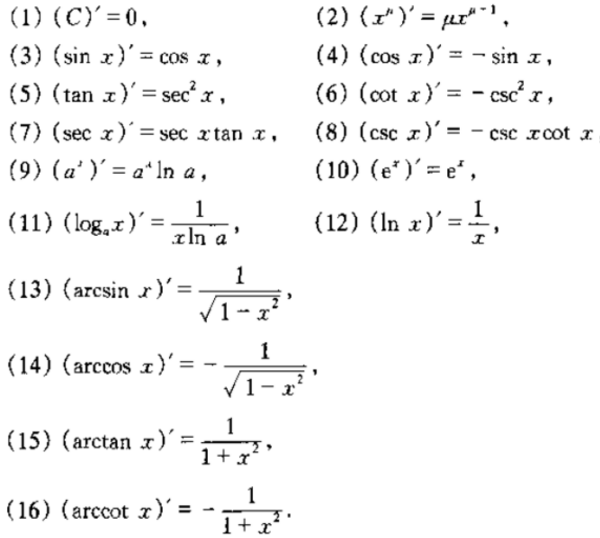 导数公式及运算法则 高数常见函数求导公式
导数公式及运算法则 高数常见函数求导公式
600x538 - 84KB - PNG
 高中复合函数求导例题
高中复合函数求导例题
500x466 - 19KB - JPEG
 简单复合函数的求导法则PPT
简单复合函数的求导法则PPT
1080x810 - 67KB - JPEG
 8-5隐函数的求导公式
8-5隐函数的求导公式
1080x810 - 179KB - JPEG
 复合函数求导ppt课件(共25页)
复合函数求导ppt课件(共25页)
661x546 - 181KB - JPEG
 隐函数的求导公式
隐函数的求导公式
1080x810 - 50KB - JPEG
 7-4 多元复合函数求导
7-4 多元复合函数求导
1080x810 - 119KB - JPEG
函数求导相关问答
简介:链式法则(英文chain rule)是微积分中的求导法则,用以求一个复合函数的导数。所谓的复合函数,是指以一个函数
简介:对于双曲函数shx,chx,thx等以及反双曲函数arshx,archx,arthx等和其他较复杂的复合函数求导时通过查阅导数表
基本函数求导公式- 答: y=x^n, y'=nx^(n-1) y=a^x, y'=a^xlna y=e^x, y'=e^x y=log(a)x ,y'=1/x lna y=lnx y'=1/x y=sinx y'=cosx y=cosx y'=-sinx y=tanx y'=1/
函数求导? 是什么意思- 答:用公式f'(x)=lim △x→0 (f(x+△x)-f(x))/△x f'(x)就是f(x)的导函数了 例如:f(x)=x 那么你用这公式就可以算到f'(x)=1 求极限你应该学过吧,没学过的话不知道
三角函数求导公式- 答: ③ (sinx)' = cosx (cosx)' = - sinx (tanx)'=1/(cosx)^2=(secx)^2=1+(tanx)^2 -(cotx)'=1/(sinx)^2=(cscx)^2=1+(cotx)^2 (secx)'=tanx·secx (cscx)'
指数函数求导- 答: 1.y=c(c为常数) y'=0 2.y=x^n y'=nx^(n-1) 3.y=a^x y'=a^xlna y=e^x y'=e^x 4.y=logax y'=logae/x y=lnx y'=1/x 5.y=sinx y'=cosx 6.y=cosx
函数求导的意义是什么?- 答:函数求导主要是研究函数值随自变量的值的变化而变化的趋势,如果导数小于零,那么函数单调递减,如果导数大于零,那么函数单调递增。
关于高数中隐函数求导的问题- 答:也就是无法写出y=f(x)的形式,如 y + siny = ln(x + y) + 3,解100辈子也解不出来!!这样的函数叫做 隐函数(implicit function). 4、碰到隐函数时,记住y是x的函数,我们求导是对x求导,
指数函数求导- 答:根据求导公式a^x'=a^xlna f(x)‘=2^xln2-2^(1-x)ln2 =ln2[2^x-2^(1-x)] f(x)‘=0时,函数有极值,此时2^x-2^(1-x)=0,有x=1-x ,即x=1/2时导数等于0, x<1/2时 导数小于
隐函数求导问题。- 答:以外,那个是要求的)。 说极端点,你可以认为y' 和y是两个完全不相干的函数。例如sinx和cosx就是两个完全不同的函数。 至于这个导数怎么应用,实际上很简单: 我们求导是
隐函数如何求导- 答:1、通常的隐函数,都是一个既含有x又含有y的方程,将整个方程对x求导; 2、求导时,要将y当成函数看待,也就是凡遇到含有y的项时,要先对y求导,然后乘以y对x 的导数,也就是说
三角函数求导- 答:y=(cosx)^sinx(1) 等价于lny=sinx*ln(cosx) (2) 将上式(2)两边求导、 1/y(dy/dx)=cosx*ln(cosx)-(sinx*sinx/cosx) (3) 在将(1)带入(3)既可以求解。
 基本初等函数求导公式与微分公式
基本初等函数求导公式与微分公式 初等函数求导PPT_word文档在线阅读与下载_无忧文档
初等函数求导PPT_word文档在线阅读与下载_无忧文档 高等数学入门--反函数的求导法则(上)
高等数学入门--反函数的求导法则(上) 复合函数求导公式
复合函数求导公式 函数求导公式三角函数导数公式sec 请问三角函数怎么求导函数比如说y=cosx
函数求导公式三角函数导数公式sec 请问三角函数怎么求导函数比如说y=cosx  复合函数求导的一题:u=x-y,v=x+y,z=f(u,v) ez\/ex=ez\/eu+ez\/ev,两边对x求偏导数得(这步怎么算的) (看得清么)
复合函数求导的一题:u=x-y,v=x+y,z=f(u,v) ez\/ex=ez\/eu+ez\/ev,两边对x求偏导数得(这步怎么算的) (看得清么) 后高考时代1 基本初等函数求导公式推导2
后高考时代1 基本初等函数求导公式推导2 幂函数求导公式
幂函数求导公式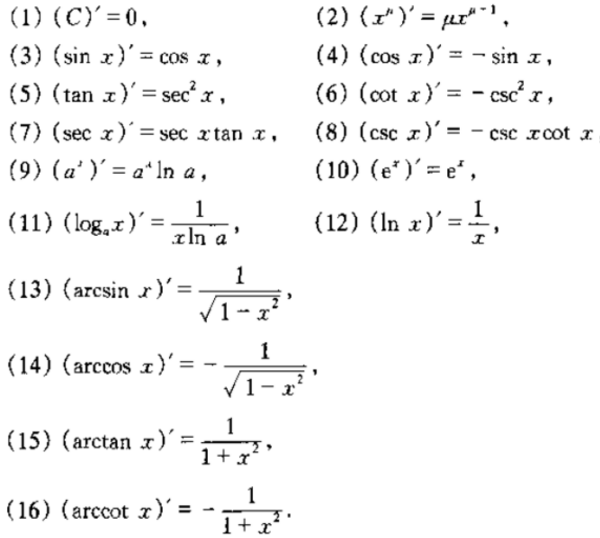 导数公式及运算法则 高数常见函数求导公式
导数公式及运算法则 高数常见函数求导公式 高中复合函数求导例题
高中复合函数求导例题 简单复合函数的求导法则PPT
简单复合函数的求导法则PPT 8-5隐函数的求导公式
8-5隐函数的求导公式 复合函数求导ppt课件(共25页)
复合函数求导ppt课件(共25页) 隐函数的求导公式
隐函数的求导公式 7-4 多元复合函数求导
7-4 多元复合函数求导