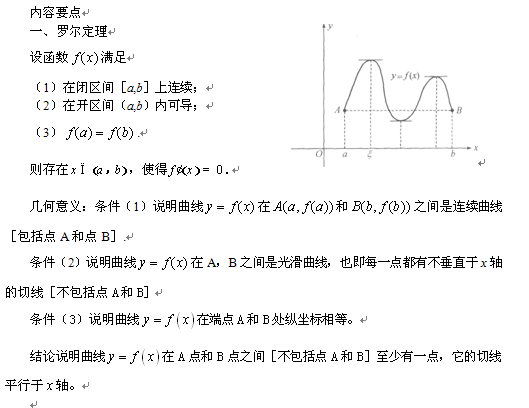
 新东方考研数学:高数基础之微分中值定理
新东方考研数学:高数基础之微分中值定理
529x408 - 22KB - PNG
 第三章 微分中值定理与导数应用单元测试
第三章 微分中值定理与导数应用单元测试
959x2548 - 339KB - PNG
 第章微分中值定理及其应用.doc
第章微分中值定理及其应用.doc
860x1215 - 82KB - PNG
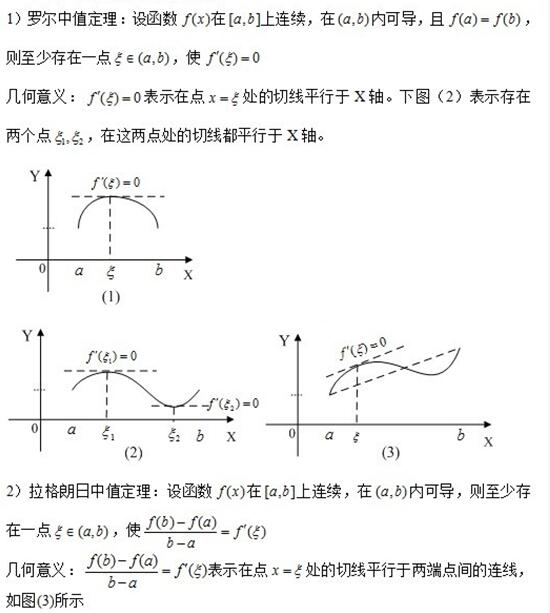 考研数学微分中值定理关联分析
考研数学微分中值定理关联分析
550x613 - 37KB - JPEG
 第四章 微分中值定理和导数的应用
第四章 微分中值定理和导数的应用
1241x949 - 895KB - PNG
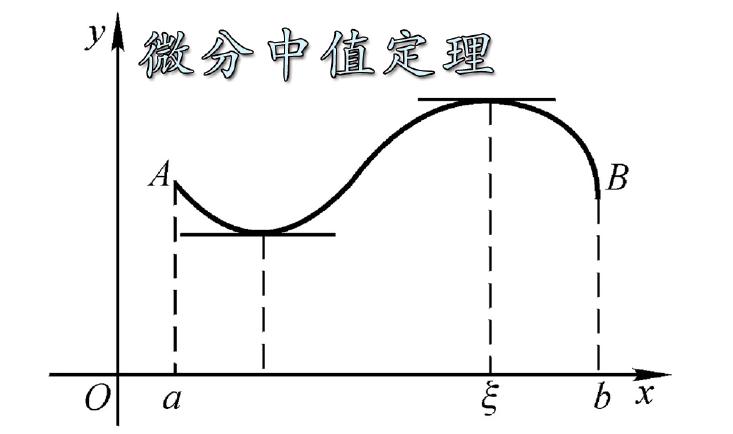 微分中值定理的应用
微分中值定理的应用
733x434 - 47KB - JPEG
 .微分中值定理
.微分中值定理
960x720 - 74KB - JPEG
 微分中值定理
微分中值定理
695x517 - 400KB - PNG
微分中值定理关系浅析
954x1478 - 133KB - PNG
 关于微分中值定理的一个注记
关于微分中值定理的一个注记
1449x1990 - 595KB - PNG
 2011年考研数学高数预测:微分中值定理
2011年考研数学高数预测:微分中值定理
550x508 - 42KB - JPEG
 微分中值定理及其应用
微分中值定理及其应用
1449x2120 - 475KB - PNG
 微分中值定理课件
微分中值定理课件
1080x810 - 146KB - JPEG
三大微分中值定理的应用
959x1357 - 205KB - PNG
微分中值定理关系浅析
954x1473 - 376KB - PNG