
典型例题分析1 :
因子分解: xy 2、4 xy4x =
解: xy2-4xy4x=x(y2-4y4)=x(y-2)2。
回答是x(y﹣2)2
试点分析:
提出公因子法和公式法的综合运用
问题分析:
首先提取公开因子x,根据完全平方式进行二次分解
反省问题:
本问题考察了公开因子法、公式法的分解因子。 提取公开因子后,应用完全平方式进行二次分解,彻底分解

典型例题分析2 :
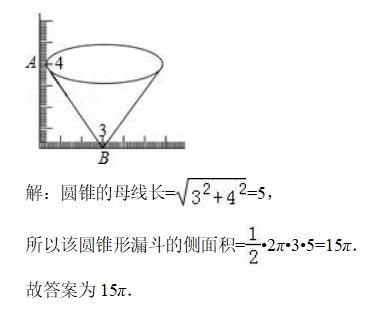
用圆锥形漏斗,某同学用三角波测量高度尺寸
这个圆锥形漏斗的侧面积
试点分析:
圆锥计算
问题分析:
如果根据图中数据得到的圆锥的高度为4,底面圆的半径为3,则根据计算定理算出母线长度为5,使用圆锥的侧面展开图成为扇形,该扇形的弧长与圆锥底面的周长相等,扇形的半径通过圆锥的母线长度和扇形的面积式求出.

典型例题分析3 :
如图所示,由一个半圆和抛物线的一部分包围的封闭图形称为“果圆”。 已知的点a、b、c、d分别是“果圆”与坐标轴的交点,抛物线的解析式是y=x2﹣2x﹣3,AB是半圆的直径,该“果圆”被y轴切断的弦CD的长度为


试点分析:
二次函数综合问题
问题分析:
连接AC、BC的抛物线的解析式可以求出a、b、c的坐标,进而求出AO、BO、DO的长度,在直角三角形ACB中,利用投影定理求出CO的长度,进而求出CD的长度.
反省问题:
本问题是二次函数综合问题型,主要考察抛物线与坐标轴的交点问题、一次二次方程、圆周角定理、投影定理,阅读问题信息,理解“果圆”的定义是解决问题的关键