一、指导思想
二、班级和学情分析本学期负责八(3)、八(4)班的数学教育,二班学生男女比例适中,经过七年级的学习,学习过程和学习方式有很大变化。 他们的优点是对新事物产生兴趣,新的欲望强烈,喜欢用手操作的活动,缺点是自觉性不高,注意力不集中。 两班数学成绩存在不均匀的问题。 在今后的教育中,我将根据这些特点,切实进行教育,努力进行人才教育
三、教材整体(章)分析第一章:本章内容认识三角形、三角形的二等分线和中线、三角形的高度、全等三角形、三角形全等条件,建立三角形。
第二章:本章内容包括等腰三角形、等腰三角形的性质、等腰三角形的判定、等腰三角形、直角三角形、座股定理、直角三角形的全等判定。
第三章:本章的内容是一次不等式和不等式组的学习。
第四章:本章的主要学习内容是探索确定位置的方法、平面直角坐标系、坐标平面内的图形变换
第五章:主要内容是常量和变量、识别函数、一次函数、一次函数的图像、一次函数的应用
四、教学目标第一章:了解三角形的初步知识①三角形的概念,用符号和字母表示三角形,了解三角形分类的任意两边之和大于第三边的性质,利用这些性质解决角度大小比较和计算的简单问题。 ②使用中线、二等分线和理解高概念的测量仪、三角尺等工具,描绘三角形的中心线、二等分线、高度。 ③理解全等图形的概念,通过重叠等方法来判定两个三角形的全等的三角形的全等概念,探索并把握两个三角形的全等条件,在简单的情况下判定两个三角形的全等条件,了解三角形的稳定性的角度之间,线段间的相互关系通过全等的性质来判定。 ④理解线段垂直平分线的概念,理解线段垂直平分线上的点到线段两端的距离相等,理解平分线上的点到角两侧的距离相等,用圆规制作平分线和线段中垂线,用直尺和圆规制作角与已知角相同,用直尺和圆规制作三角形。
第二章:特殊三角形①理解等腰三角形相关概念②探索并把握等腰三角形的性质③探索三角形为等腰三角形的条件④理解等腰三角形的性质和三角形为等边三角形的条件④理解直角三角形相关概念⑤探索并把握直角三角形的性质⑥使用钩子定理来解决简单的问题
第三章:一次不等式①经历一些实际问题抽象化为不等式的过程,体会不等式也是一个描述现实世界中量与量关系的有效数学模型,进一步发展符号感。 ②从具体问题中的大小关系可以知道不等式的含义。 ③通过类比、推测、验证发现不等式基本性质的探索过程,掌握不等式的基本性质。 ④可解不等式(组)解和解集意义的简单一次不等式,求解一次不等式解集可用轴表示的一次不等式组,初步体会在数学轴上确定该解集的数形耦合思想。 ⑤根据具体问题的数量关系,列举一次不等式(组),解决简单的实际问题,根据具体问题的实际含义,可以验证结果是否合理。 ⑥初步体会不等式、方程式、函数之间的内在联系和差异。
第四章:图形和坐标①在现实场景中感受到确定物体位置的方法,可以用不同的方法确定物体位置②识别平面正交坐标系,在可以描绘的给定正交坐标系中,从坐标描绘点的位置,从点的位置写入该坐标③可以在方格纸上制作适当的正交坐标系, 描述物体位置④在同一正交坐标系中,经历了探索图形上点坐标变化和图形变换影响⑤位置的过程和与他人合作交流的过程,进一步发展了数形结合意识、对美的鉴赏意识。
第五章:一次函数①经历常数和变量、函数、一次函数等概念的抽象概括过程,体会函数的模型思想,进一步发展学生的抽象思维能力,经历一次函数的图像及其性质的探索过程,在合作交流活动中发展学生的意识和能力。 ②经历一次函数及其图像解决实际问题的过程,经历发展学生数学应用能力的函数图像信息识别和应用过程,发展学生的形象思维能力。 ③初步理解函数概念初级函数与理解其影像性质的方程式与函数的关系。 ④根据给定的信息决定一次函数公式,制作一次函数的图像,利用它可以解决简单的实际问题。
五、各章重要难点第一章三角形的初步知识:全等三角形是本章教学的重点,根据已知条件判定两个三角形的全等性,根据全等三角形的性质判定图形的边与边、角与角的关系,说明理由是本章教学的难点。
第二章特殊三角形:重要的是特殊三角形包括等腰三角形、等边、直角三角形的性质,难点在于利用这些性质来解决问题
第三章一次不等式:重点是一次不等式和一次不等式组,难点是一次不等式的实用(实际问题对解集的影响)和建模。
第四章图形与坐标:重点是从坐标角度让学生理解图形的平移、轴对称的数学内涵,难点是培养数形结合思想和体验运动的观点
第五章初级函数:重点是关于初级函数的知识,难点是初级函数的应用
六、各章具体的教学方法和措施,为了更好地促进学生的学习,对学生的具体情况,特别制定以下措施
(1)为学生提供现实、有趣、有挑战性的学习素材。 数学知识的学习目标是从学生的实际中,在他们熟悉或感兴趣的问题的情况下引入学习主题,开展数学探索。
(二)为学生提供探索、交流的时间和空间;。 根据学生的知识背景和活动经验,提供多种操作、思考和交流的学习机会。 同时,要求学生通过自主的探索和同伴的交流,形成新的知识,总结规律,记述概念,总结学习内容等。 利用章后回顾与思考,总复习,通过思考与交流,整理学生学到的知识,构建符合个人认知特征的知识结构。
(3)给出数学知识的形成和应用过程。 利用教材中的“问题方案-模型的构建-解释、应用和展开”模型进行展开。 对所有新知识的学习设定情况,以问题排列的形式开展探索和交流,让学生体验“做数学”的过程。
(4)满足不同学生发展的需要。 利用《读一读》栏目提供的关于数学史料和背景知识的介绍、有趣或有挑战性的问题讨论、关于数学知识扩展的介绍等,为学生提供更多理解数学、研究数学的机会。 对学生进行阶层教育的“练习一练”的内容是对全体学生熟悉、强化新学生的知识、技能和方法,或者加深对相关知识和方法的理解,“试一试”,不需要只对有特殊数学学习需要的学生理解和研究知识和方法,让全体学生完成它。
(5)逐步渗透重要的数学思想方法。 在学习过程中,让学生们感受和应用理解相关的数学思想方法
(6)希望在教学中培养学生在学习数学解决问题过程中充分利用计算机,用现代科学技术解决实际问题的意识和能力。 他们为了不从事很多复杂反复的机械性操作活动,将更多的精力投入到有意义的探索活动中。
(7)在教学中尽量使用不同的教学媒体,包括模型、挂图、电影、录像带、软件等,丰富学生感知识别对象的途径,促进他们接近数学,更好地理解数学,在数学学习中取得更多成功。
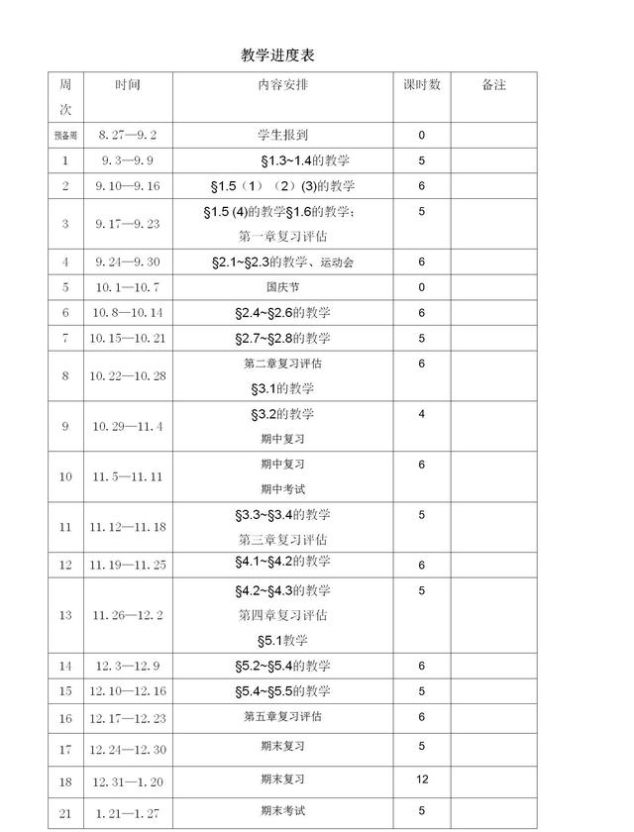
七、教育时间表