
sias概率统计简明总复习题.doc
870x1229 - 70KB - PNG

4183 概率论与数理统计(经管类) 概率论与数理
993x1404 - 81KB - PNG

(精选)逻辑学教程 全套课件课件.ppt
1152x864 - 668KB - PNG

离散数学总结.ppt文档全文免费阅读、在线看
1152x864 - 106KB - PNG

习题课知识点总结及习题答案.pdf
800x1131 - 244KB - PNG

第二章 数理统计的基本概念.ppt下载-支持高清
1152x864 - 201KB - PNG
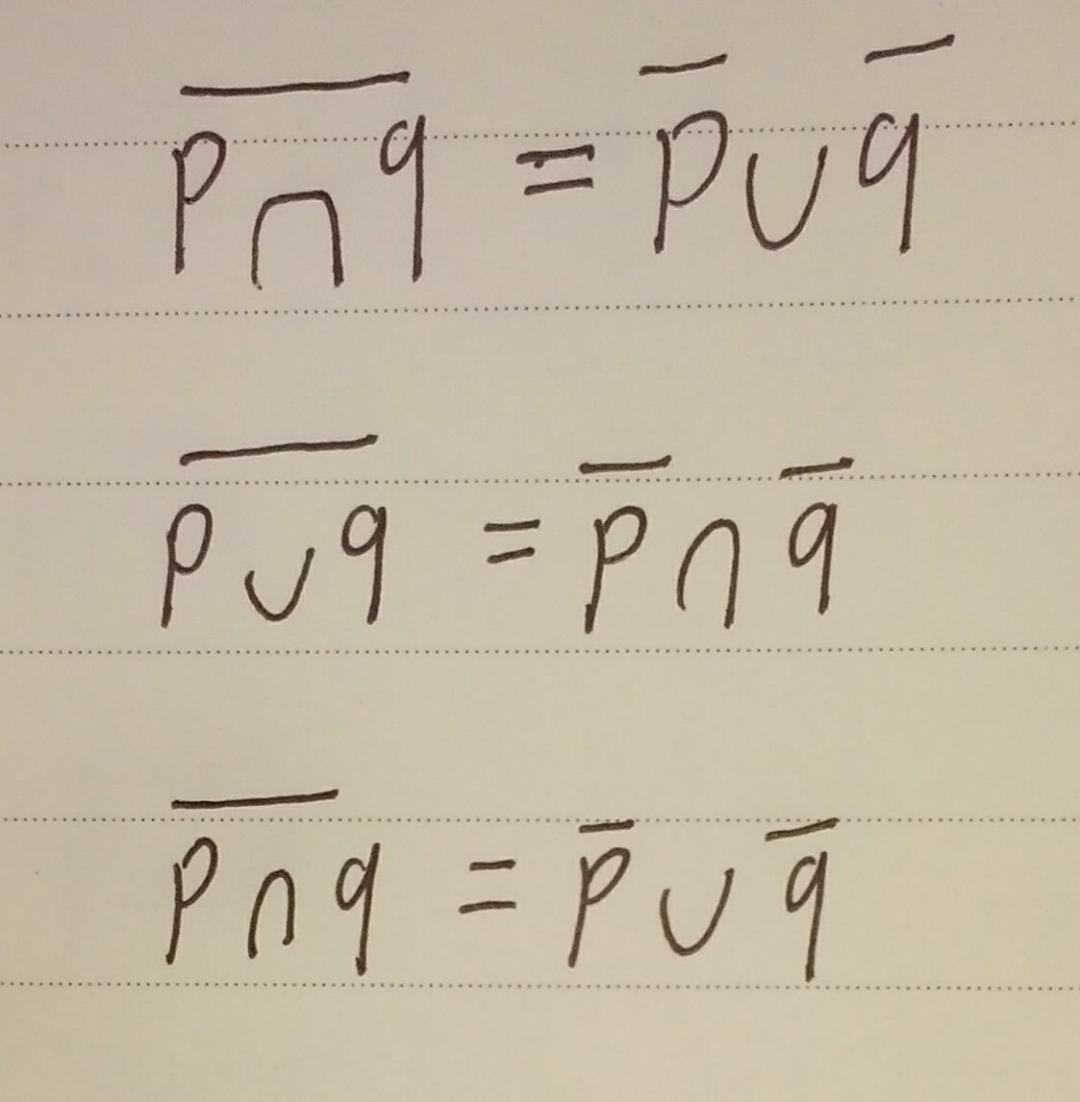
颜文字 - 最新问答 - 知乎
1080x1102 - 672KB - PNG

2019考研管理类联考逻辑知识点:两个德摩根律
586x430 - 45KB - JPEG

019考研管理类联考逻辑知识点:两个德摩根律(
586x430 - 53KB - JPEG

(离散数学结构试题集2011.doc
141x200 - 6KB - PNG

(2017考研数学必看:概率各章常考题型全.doc
141x200 - 7KB - PNG

概率论与数理统计期末必备复习资料.ppt
1152x864 - 281KB - PNG

离散数学结构试题集1-4.doc
993x1404 - 122KB - PNG

随机事 件和样本空间.ppt
1152x864 - 71KB - PNG

命题逻辑第一课 命题公式与等值演算精要.ppt
141x200 - 3KB - JPEG
简介:德·摩根律是属于逻辑学的定律。 德·摩根定律(或称德·摩根定理)是形式逻辑中有关否定所描述的系统方式中
德(yi)·摩(lian)根(meng)律(bi)的两个公式: 下面是我的一种理解方法: 我们假设事件 p = {我的钱 };事件 q = {你的钱 }; 先来看看第一个公式 (¬p∧¬q) = ¬(p∨q); 我们容易得到 :
这是概率论的问题吧。 A的逆事件与B的逆事件发生的概率等于一减去A,B同时发生的概率。 比如A事件是掷骰子出现一的概率,1/6. B事件是掷骰子出现一的概率,1/6. 则A的逆事件是出现2,3,4,5,6的概率,5/6,打字不方面,用C表示 B的逆事件是出现1.3.4.5.6的概率,5/6,用D表示 而P(C+D)=P(C)+P(D)-P(CD). 即C发生,D发生,但是要减去C和D的重合部分,容易理解涩 而这个例子,P(C+D)=5/6+5/6-4/6=1,即一定会发生的。因为C和D包含了一到六的所有数。 对应上面的式子,AB是A和B都发生的概率,即1/3,所以P(CD)=1-1/3=2/3. 你可以理解为,出现3,4,5,6的概率。 A和B不是独立的,所以P(AB)不等于0
集合运算中: 先并再补等于先补再交,先交再补等于先补再并. 简称: 并补补交,交补补并
晕从头到尾都是错的 (A∪B)-A=B-(A∩B) √这个我知道啊,我只是想问问德摩根律而已自己上网找公式别死记硬背的自己推理一边就能记住了一边推不明白就一直推理下去直到
德摩根律的两个逻辑等价式非常重要。它们告诉我们怎么去否定合取和析取。特别地,等价式┐(p∨q)≡┐p∧┐q说明,析取的否定是由各分命题的否
在命题逻辑和逻辑代数中,德·摩根定律(或称德·摩根定理)是关于命题逻辑规律的一对法则。奥古斯塔斯·德·摩根首先发现了在命题逻辑中存在着下面这些关系:非(P 且 Q) = (非 P) 或 (非 Q)非(P 或 Q) = (非 P) 且 (非 Q)德·摩根定律在数理逻辑的定理推演中,在计算机的逻辑设计中以及数学的集合运算中都起着重要的作用。 他的发现影响了乔治·布尔从事的逻辑问题代数解法的研究。这巩固了德摩根作为该规律的发现者的地位,尽管亚里士多德也曾注意到类似现象,且这也为古希腊与中世纪的逻辑学家熟知。
德摩根律是我们演绎推理考试时经常考的一个知识点,讲的其实是两个等价公式,对于这部分的学习,重要的是要明白这两个等价如何得来的,可以帮助
德摩根律徳摩根律(对偶律)德摩根律是属于逻辑学的定律。德摩根定律(或称德摩根定理)是形式逻辑中有关否定所描述的系统方式中的逻辑运算符对偶对的一系列法则。由此引
德 摩 根 律 toose12347|2018-07-02 马上扫一扫 手机打开 随时查看 手机打开 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载