相似对角化_可相似对角化

求正交变换矩阵Q式的矩阵相似对角化!_360问

418x743 - 36KB - JPEG

2017考研数学线性代数考点预测

750x256 - 565KB - PNG

2018考研数学中相似矩阵及相似对角化相关问

554x611 - 21KB - PNG

有理矩阵有理相似对角化计算机实现.doc

993x1404 - 146KB - PNG

相似对角化求矩阵的n次幂,最后少了系数是怎么

600x326 - 29KB - PNG

2016考研数学:矩阵的相似对角化

591x276 - 36KB - JPEG

线性代数,相似矩阵,对角化_突袭网-提供留学,移

390x520 - 28KB - JPEG

2016考研数学矩阵相似对角化.doc

141x200 - 8KB - PNG

矩阵A=201 31x 405可相似对角化,求x?答案是x

581x1032 - 58KB - JPEG

相似矩阵、相似对角化.ppt

141x200 - 6KB - JPEG

2018考研数学中相似矩阵及相似对角化相关问

521x416 - 52KB - PNG

相似矩阵对角化说课-学路网-学习路上 有我相伴

1080x810 - 61KB - JPEG

5 第五章 矩阵的相似对角化 第六章 二次型 作业

959x1361 - 132KB - PNG

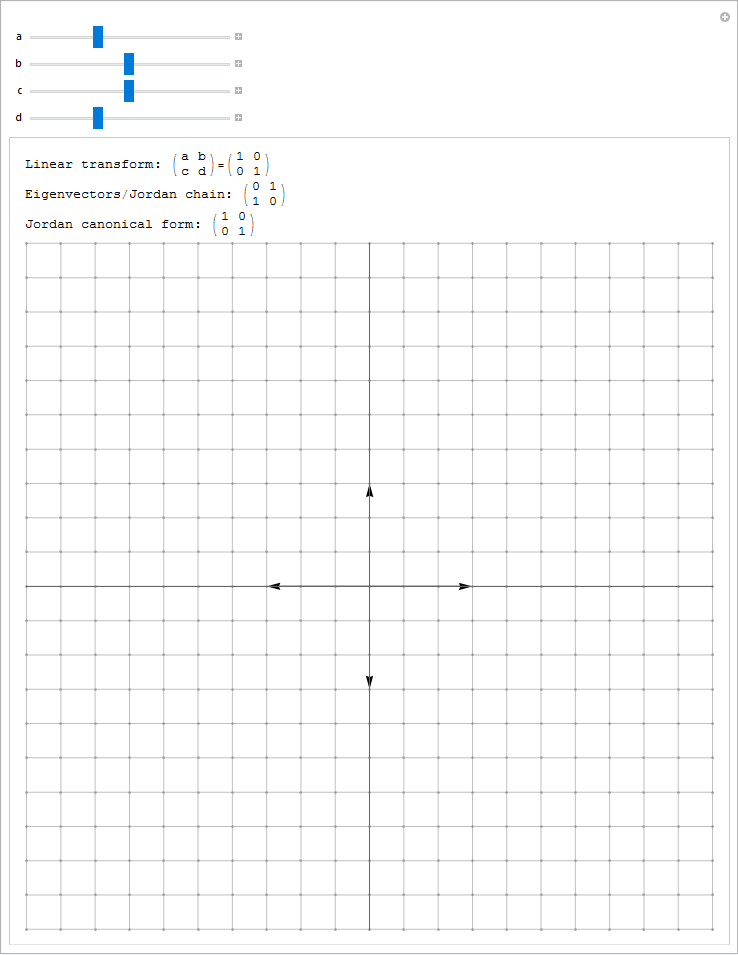
如何理解矩阵不能相似对角化?

738x955 - 81KB - JPEG

2018考研数学中相似矩阵及相似对角化相关问

565x788 - 39KB - PNG

23.6.2相似对角化 猿飞日斩是傻|2018-06-30 |举报 共享文档 共享文档是百度文库用户免费上传的可与其他用户免费共享的文档,具体共享方式由上传人自由设定。了解文档类型

线性代数-矩阵相似对角化 yangyiwangsai|2011-02-11 |举报 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载特权礼包的其他会

相似矩阵与相似对角化 超级网爸上传于2010-09-15|暂无评价|0|0|文档简介|举报 相似矩阵与相似对角化 大小:632.50KB 免费 下载 收藏此文档 登录百度文库,专享文档复制特权

不一定,要A能相似对角化,必须要找到使其对角化的矩阵,这个矩阵式由A的特征向量构成的, Λ=p^-1Ap,而p必须可逆,即对于n阶矩阵要有n个线性无关的特征向量;书上给出的两种

能够相似对角化有两种可能 第一种:有N个不同的特征值 第二种:有相同的特征值,N重特征值有N个线性无关的特征向量。 两种情况合二为一就是:有N个线性无关的特征向量。 所以说,A可相似对角化的话,n阶方阵A的n个特征值不一定全都不相等,可能包含有重根在里面。 “可是A有n个互不相等的特征向量,也能推出A可相似对角化。但是!反过来就不行了..” 不明白你的意思

做线代的时候问“可否相似对角化”和“可否对角化”解答过程都是一个套路。 阅读原文 关于对角化和相似对角化有什么区别嘛。有4名研友在考研帮APP发表了观点。 下

P^-1AP = 对角矩阵 正交对角化要求 P 是正交矩阵, 即P可逆且 P^-1 = P^T 即是相似变换又是合同变换, 用于二次型 可逆矩阵相似对角化 一般考虑的是方阵, 并不要

n阶方阵可进行对角化的充分必要条件是: 1.n阶方阵存在n个线性无关的特征向量 推论:如果这个n阶方阵有n个不同的特征值,那么矩阵必然存在相似矩阵 2.如果阶n方

【请问】怎样判断一个矩阵是否可以相似对角化下面的矩阵可以吗?A 1 2 1 0 3 0 0 0 0B 1 2 1 0 1 0 0 0 3详见:

矩阵A可相似对角化的充分条件是:A有n个不同的特征值。可是同一特征值对应的特征向量有可能线性无关,即n个不同的特征值就有可能对应有大于n个的线性无关的特征向量,书