叉乘_点乘叉乘

向量叉乘求导公式

1080x810 - 72KB - JPEG

向量叉乘(Cross_Product)

1080x810 - 41KB - JPEG

关于向量的叉乘右手定则判方向

611x411 - 41KB - JPEG

叉乘为什么符合反交换率_360问答

600x338 - 15KB - JPEG

向量点乘(内积)和叉乘(外积、向量积)概念及几

621x367 - 30KB - JPEG

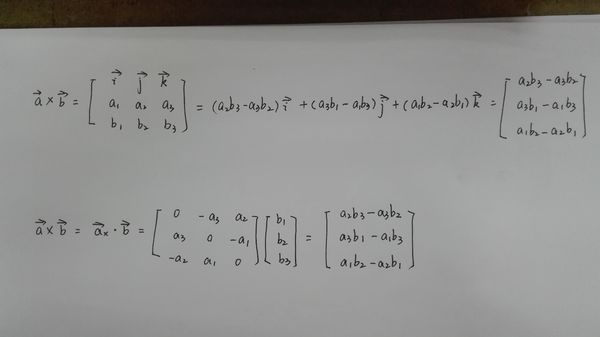
向量中叉乘和点乘怎么转换的?我看到书里上一

600x337 - 14KB - JPEG

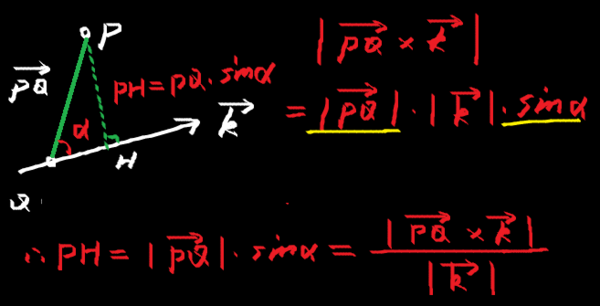
空间距离公式的分子到底是点乘还是叉乘,怎么

600x306 - 54KB - PNG

三矢量叉乘展开成点乘的公式如何证明? - 知乎

638x279 - 34KB - PNG

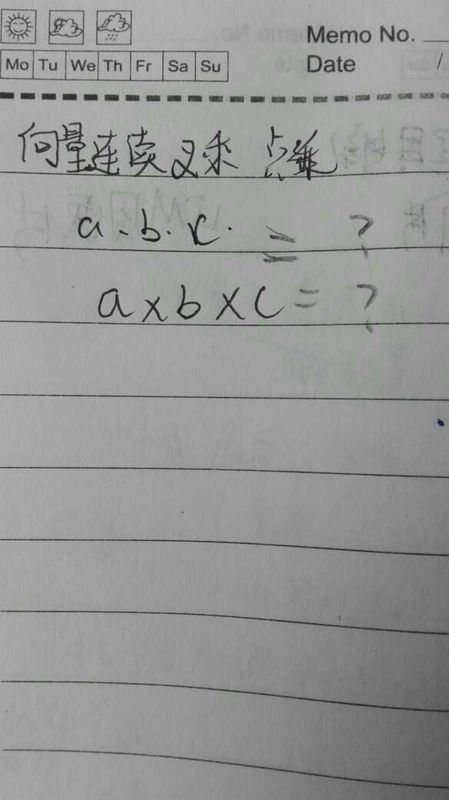
向量连续点乘,叉乘,有没有这种运算?等于几啊

449x800 - 34KB - JPEG

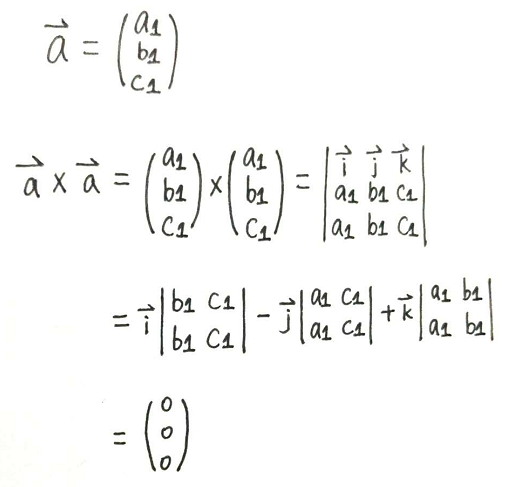
两个相同空间向量叉乘等于什么…_360问答

510x487 - 91KB - PNG

高中物理的左手右手定则 能不能用叉乘的思想

528x623 - 47KB - JPEG

这个算式过程怎么算?就是一个数叉乘一个向量

600x800 - 54KB - JPEG

最好的高数下册(同济版)复习提纲.doc

141x200 - 13KB - PNG

maple18中矩阵点乘、叉乘问题 求知实现图片

935x456 - 15KB - PNG

向量问题。叉乘和三个向量点乘的问题。

596x604 - 30KB - JPEG

简介：向量积，也被称为叉积（即交叉乘积）、外积，是一种在向量空间中向量的二元运算。与点积不同，它的运算结

叉乘(向量的外积)是物理里面常常用到的概念,它是由两个向量得到一个新的向量的运算。一般我们都是从几何意义下手:向量\(\vec a\)和\(\vec b\)叉乘,得到一个垂直于\(\vec a\)和

1. 在一般的常识或者教科书中规定叉乘只有3d才拥有,其实2d也可以拓展出来一个叉乘形式,而且非常有用。 拓展方式:假设有两个2d向量a,b,我们直接把他们视为3d向量,z轴补

向量积,也被称为叉积(即交叉乘积)、外积,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个伪向量而不是一个标量。并且两个向量的叉积与这两个向量都垂直。"正确"的向量由向量空间的方向确定,即按照给定直角坐标系(i, j, k)的左右手定则。若 (i, j, k)满足右手定则,则 (a, b, a×b)也满足右手定则;或者两者同时满足左手定则。一个简单的确定满足"右手定则"的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。由于向量的叉积由坐标系确定,所以其结果被称为伪向量。

叉乘,也叫向量的外积、向量积。顾名思义,求下来的结果是一个向量,记这个向量为c。 |向量c|=|向量a×向量b|=|a||b|sin<a,b> 向量c的方向与a,b所在的平面垂直,且方向要用"右手法则"判断(用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向)。 因此 向量的外积不遵守乘法交换率,因为向量a×向量b= - 向量b×向量a 在物理学中,已知力与力臂求力矩,就是向量的外积,即叉乘。 将向量用坐标表示(三维向量), 若向量a=(a1,b1,c1),向量b=(a2,b2,c2), 则 向量a×向量b= | i j k | |a1 b1 c1| |a2 b2 c2| =(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1) (i、j、k分别为空间中相互垂直的三条坐标轴的单位向量)。

1. 在一般的常识或者教科书中规定叉乘只有3d才拥有,其实2d也可以拓展出来一个叉乘形式,而且非常有用。 拓展方式:假设有两个2d向量a,b,我们直接把他们视为3d向量,z轴补0

点乘是向量的内积 叉乘是向量的外积例如:点乘:点乘的结果是一个实数 a·b=|a|·|b|·cos<a,b <a,b表示a,b的夹角 叉乘:叉乘的结果是一个向量 当向量a和b不平行

点乘,也叫数量积。结果是一个向量在另一个向量方向上投影的长度,是一个标量。 叉乘,也叫向量积。结果是一个和已有两个向量都垂直的向量。 以我比较熟悉的图

a叉乘b的计算过程应该是怎样的,求详解 作业帮用户 数学 2017-10-21 会用行列式吗?给你一个公式: 设a=(X1,Y1,Z1),b=(X2,Y2,Z2), a×b=(Y1Z2-Y2Z1,Z1X2-Z2X1,X1Y2-X2Y1)