对数函数变换公式大全_对数函数变换公式

【积化和差通用】求高中数学中对数的常用变换

650x919 - 57KB - JPEG

中公考研2018考研管综数学常用公式考前预测

575x485 - 41KB - PNG

【积化和差通用】求高中数学中对数的常用变换

650x365 - 27KB - JPEG

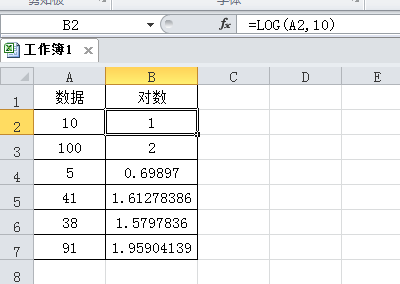
如何在Excel中将一列数据都进行对数变换

400x284 - 6KB - PNG

电大复变函数与积分变换重点公式归纳小抄.do

794x1123 - 36KB - PNG

已知函数f(x)=$\frac{mx}{lnx}$.曲线y=f(x)在点(e2

629x217 - 72KB - PNG

e的全称是自然对数的底_中华文本库

892x587 - 5KB - PNG

高一二三的同学,想复习指数函数对数函数的可

264x130 - 7KB - JPEG

复数及拉普拉斯变换的复习.ppt

141x200 - 5KB - JPEG

复数-拉普拉斯变换的复习.ppt

141x200 - 7KB - JPEG

伟大的不仅仅是傅里叶是个数学公式,别的方面

640x360 - 25KB - JPEG

图像相似度测量与模板匹配总结_「电脑玩物」

531x351 - 32KB - PNG

第4章系统安全预测技术概述.ppt

960x720 - 62KB - JPEG

mathmatica运算遇到问题 求助 - 计算模拟 - 小木

397x320 - 31KB - JPEG

高中数学第三章指数函数和对数函数35对数函

642x556 - 40KB - JPEG

对数函数有多少公式? 下载作业帮 扫二维码下载作业帮 4亿+用户的选择 下载作业帮安 公式:log(A)M=log(b)M/log(b)A (b 0且b≠1) (6)log(a^n)M^m=(m/n)log(a)M (7)对数恒等式

对数函数log的各种公式 下载作业帮 扫二维码下载作业帮 拍照搜题,秒出答案,一键查看所有搜题记录 下载作业帮安装包 扫二维码下载作业帮 拍照搜题,秒出答案,一键查看所有

对数函数图像变换 很傻72|2018-06-30 |举报 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载特权礼包的其他会员用户可用专业

对 数 函 数 图 象 变 换 obama工口上传于2011-08-24|质量:4.6分|721|86|暂无简介|举报 手机打开 试读已经结束,如果需要继续阅读或下载,敬请购买 ￥0元 购买 大小:284.50KB

简介：如果a^x=N(a>0,且a不等于1)，则数x叫做以a为底N的对数，记做x=log（a）（N） ，其中a要写于log右下。对数性

这个就很多了 我举几个例子 logbM=logaM/logab(换底公式) 1/logab 可将1转换为底的对数 即logaa/logab(a为底a的对数)然后将公共的底数去掉 得logba=1/logab lga+lgb=lg(a

对数的性质及推导 用^表示乘方,用log(a)(b)表示以a为底,b的对数 *表示乘号,/表示除号 定义式: 若a^n=b(a>0且a≠1) 则n=log(a)(b) 基本性质: 1.a^(log(a)(b))=b 2.log(a)(MN)=log(a)(M)+log(a)(N); 3.log(a)(M/N)=log(a)(M)-log(a)(N); 4.log(a)(M^n)=nlog(a)(M) 推导 1.这个就不用推了吧,直接由定义式可得(把定义式中的[n=log(a)(b)]带入a^n=b) 2. MN=M*N 由基本性质1(换掉M和N) a^[log(a)(MN)] = a^[log(a)(M)] * a^[log(a)(N)] 由指数的性质 a^[log(a)(MN)] = a^{[log(a)(M)] + [log(a)(N)]} 又因为指数函数是单调函数,所以 log(a)(MN) = log(a)(M) + log(a)(N) 3.与2类似处理 MN=M/N 由基本性质1(换掉M和N) a^[log(a)(M/N)] = a^[log(a)(M)] / a^[l

基本性质: 1、a^(log(a)(b))=b 2、log(a)(a^b)=b 3、log(a)(MN)=log(a)(M)+log(a)(N); 4、log(a)(M÷N)=log(a)(M)-log(a)(N); 5、log(a)(M^n)=nlog(a)(M) 6、log(a^n)M=1/nlog(a)(M) 推导 1、因为n=log(a)(b),代入则a^n=b,即a^(log(a)(b))=b。 2、因为a^b=a^b 令t=a^b 所以a^b=t,b=log(a)(t)=log(a)(a^b) 3、MN=M×N 由基本性质1(换掉M和N) a^[log(a)(MN)] = a^[log(a)(M)]×a^[log(a)(N)] =(M)*(N) 由指数的性质 a^[log(a)(MN)] = a^{[log(a)(M)] + [log(a)(N)]} 两种方法只是性质不同,采用方法依实际情况而定 又因为指数函数是单调函数,所以 log(a)(MN) = log(a)(M) + log(a)(N) 4、与(3)类似处理 MN=M÷N 由基本性质1(换掉M和N) a^[log(

对数函数及其性质-对数的公式互化-详尽的讲解 Soulmates210|2017-11-20 |举报 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下

a^(m/n)=(n)^√(a^m) (a>0,m、n∈N*,且n>1) a^(-m/n)=1/[(n)^√(a^m)] (a>0,m、n∈N*,且n>1) log(a)[MN]=log(a)[M]+log(a)[N] (a>0 且 a≠1,M>0,N>0) log(a)[M/N]=log(a)[M]-l