对数函数公式证明_对数函数换底公式证明

求指数函数和对数函数求导公式的证明。

500x369 - 21KB - JPEG

证明对数函数换底公式,急求,在线等

562x750 - 14KB - JPEG

#高中数学# 对数函数的换底公式怎么证明?

458x800 - 22KB - JPEG

求指数函数和对数函数求导公式的证明。

500x369 - 21KB - JPEG

求指数函数和对数函数求导公式的证明。

500x250 - 19KB - JPEG

求对数换底公式步骤的讲解

434x471 - 42KB - JPEG

对数函数换底公式.ppt

1152x864 - 192KB - PNG

数学对数函数换底公式的推演如何证明

620x459 - 66KB - JPEG

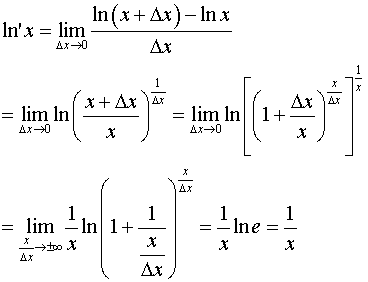
如何证明对数函数求导公式?

368x282 - 20KB - JPEG

对数函数公式

141x157 - 5KB - JPEG

对数式与对数函数复习课件.ppt

960x720 - 43KB - JPEG

[高中数学公式口诀主要为函数.doc

141x200 - 13KB - PNG

算器,颜色,复杂性,概念,考虑,教育,平等的,公式,几

1024x799 - 229KB - JPEG

算器,颜色,复杂性,概念,考虑,教育,平等的,公式,几

1023x691 - 183KB - JPEG

念,相等的,计数,小数,分母,分开,方程,表达,公式,

1024x1024 - 237KB - JPEG

关于对数函数计算公式的证明证明对数函数的计算公式logambm=logab,logam.logbn=logan.logbm,老师,希望以后能够多得到您的解答,让我对数学更有兴趣, 下载作业帮 扫二维

( R n M n Mana∈ = 3.logloglogbNNaab=对数换底公式:关于函数连续性的一条结论:一切初等函数在它们的定义区间上是连续函数 .• (二)对数函数的导数:. ) ln ( .xx11 = ′证明:设

简介：如果a^x=N(a>0,且a不等于1)，则数x叫做以a为底N的对数，记做x=log（a）（N） ，其中a要写于log右下。对数性

对数公式的推导(全) 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载特权礼包的其他会员用户可用专业文档下载特权免费下载

解答: (1) 设loga(b)=x 则a^x=b ∴ a^(mx)=b^m ∴ (a^m)^x=b^m ∴ x=log(a^m) (b^m) 即 log(a^m) (b^m)=loga(b) 如果使用换底公式,更加简单 (2)利用换底公式 loga(m)*logb(n)=(lgm/lga)*(lgn/lgb)=(lgm*lgn)/(lga*lgb) loga(n)*logb(m)=(lgn/lga)*(lgm/lgb)=(lgm*lgn)/(lga*lgb) ∴ loga(m)*logb(n)=loga(n)*logb(m)

13.参考 2.对数函数的导数公式的推导 330987565|2018-06-28 |举报 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载特权礼包

设loga=m,a=10^mlogb=n,b=10^nab=10^(m+n)则logab=m+n=loga +logb

基本性质: 1、a^(log(a)(b))=b 2、log(a)(a^b)=b 3、log(a)(MN)=log(a)(M)+log(a)(N); 4、log(a)(M÷N)=log(a)(M)-log(a)(N); 5、log(a)(M^n)=nlog(a)(M) 6、log(a^n)M=1/nlog(a)(M) 推导 1、因为n=log(a)(b),代入则a^n=b,即a^(log(a)(b))=b。 2、因为a^b=a^b 令t=a^b 所以a^b=t,b=log(a)(t)=log(a)(a^b) 3、MN=M×N 由基本性质1(换掉M和N) a^[log(a)(MN)] = a^[log(a)(M)]×a^[log(a)(N)] =(M)*(N) 由指数的性质 a^[log(a)(MN)] = a^{[log(a)(M)] + [log(a)(N)]} 两种方法只是性质不同,采用方法依实际情况而定 又因为指数函数是单调函数,所以 log(a)(MN) = log(a)(M) + log(a)(N) 4、与(3)类似处理 MN=M÷N 由基本性质1(换掉M和N) a^[log(

对数公式推导过程及总结 九州清华|2018-06-26 |举报 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载特权礼包的其他会员用户

知乎的识别也是醉了。。。题主可以看一下被折叠的那个答案,那个答案相当规范。另外,遇到类似证明某函数求导公式的问题,永远要从定义入手证明。