等比求和_等比求和公式

非等差等比数列求和

562x325 - 111KB - JPEG

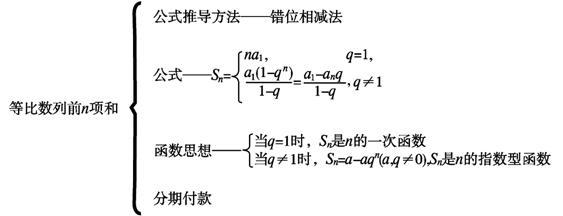
求等比数列求和公式,简单点,举个例子

563x216 - 12KB - JPEG

3.3+等比数列求和1

323x236 - 17KB - JPEG

非等差等比数列求和

572x491 - 228KB - JPEG

等比数列与求和公式及性质 .ppt

1152x864 - 211KB - PNG

等比数列求和公式 黄杰PPT_word文档在线阅读

1080x810 - 75KB - JPEG

已知数列{an}是等比数列

320x240 - 8KB - JPEG

WSP等比数列求和.ppt

1152x864 - 1176KB - PNG

等比数列求和公式推导方法_高考网

341x355 - 13KB - PNG

等差与等比数列和数列求和的基本方法和技巧.

688x972 - 32KB - PNG

等比求和_中华文本库

747x1039 - 72KB - JPEG

等比求和_中华文本库

741x1035 - 42KB - JPEG

讲座笔记|等比数列求和公式推导的策略思考[数

462x254 - 12KB - JPEG

等差数列和等比数列、求和_中华文本库

674x713 - 80KB - JPEG

等比数列求和公式推导ppt下载

806x1374 - 181KB - JPEG

等比数列公式就是在数学上求一定数量的等比数列的和的公式。另外,一个各项均为正数的等比数列各项取同底数数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数

等比数列的求和公式 叶琴1717520|2013-11-23 |举报 专业文档 专业文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买专业文档下载特权礼包的其他会员用户

1. 掌握错位相减法,求等比数列的和; 2.掌握特定公比等比数列求和的补项技巧。 享专业文档下载特权 赠共享文档下载特权 100w优质文档免费下载 赠百度阅读VIP精品版 立即

(6)在等比数列中,首项a1与公比q都不为零.注意:上述公式中an表示等比数列的第n项.等比数列求和公式推导:Sn=a1+a2+a3+.+an(公比为q) q*Sn=a1*q+a2*q+a3*q+.+an*q =a2+a

简介：等比数列求和公式为：Sn=n*a1(q=1) Sn=a1(1-q^n)/(1-q) =(a1-anq)/(1-q) （q不等于 1）等比数列等比数列的意义​一

(3) 求和公式:Sn=n*a1 (q=1) Sn=a1(1-q^n)/(1-q) =(a1-an*q)/(1-q) (q≠1) (q为比值,n为项 (3)从等比数列的定义、通项公式、前n项和公式可以推出: a1·an=a2·an-1=a3·an-2

这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0) 其中 Sum代表求和的意思, a是首项,q是比例 ,i是每项中比

1）等比数列：a（n+1）/an=q, n为自然数。 （2）通项公式：an=a1*q^（n－1）； 推广式： an=am·q^(n－m)； （3）求和公式：sn=n*a1(q=1) sn=a1(1-q^n)/(1-q) =(a1-a1q^n)/(1-q) =a1/(1-q)-a1/(1-q)*q^n ( 即a-aq^n) (前提：q不等于 1) （4）性质： ①若 m、n、p、q∈n，

首项a1,公比q a(n+1)=an*q=a1*q^(n )Sn=a1+a2+..+an q*Sn=a2+a3++a(n+1) qSn-Sn=a(n+1)-a1 S=a1(q^n-1)/(q-1)1、等比数列的意义:一个数列,如果任意的后一项与前一项的比值是同一个常数,即:A(n+1)/A(n)=q (n∈N*),这个数列叫等比数列,其中常数q 叫作公比。如:2、4、8、16.2^10 就是一个等比数列,其公比为2,可写为(A2)的平方=(A1)x(A3)。2、求和公式等比数列求和公式:Sn=n×a1 (q=1)Sn=a1(1-q^n)/(1-q) =(a1-an*q)/(1-q) (q≠1)=a1(q^n-1)/(q-1)(q为公比,n为项数)等比数列求和公式推导:Sn=a1+a2+a3++an(公比为q)q*Sn=a1*q+a2*q+a3*q++an*q=a2+a3+a4++a(n+1)Sn-q*Sn=a1-a(n+1)(1-q)Sn=a1-a1*q^nSn=(a1-a1*q^n)/(1-q)Sn=(a1-a

等比数列求和公式如下图,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0),等比数列a1≠ 0。注:q=1 时,an为常数列。利用等比数列求和公式可以快速的计算出该数列的和。求和公式推导(1)Sn=a1+a2+a3++an(公比为q)(2)q*Sn=a1*q+a2*q+a3*q++an*q=a2+a3+a4++an+a(n+1)(3)Sn-q*Sn=(1-q)Sn=a1-a(n+1)(4)a(n+1)=a1*q^n(5)Sn=a1(1-q^n)/(1-q)(q≠1)性质①若 m、n、p、q∈N,且m+n=p+q,则am×an=ap×aq;等比数列的性质②在等比数列中,依次每 k项之和仍成等比数列;③若m、n、q∈N,且m+n=2q,则am×an=(aq)^2;④ 若G是a、b的等比中项,则G^2=ab(G ≠ 0);⑤在等比数列中,首项a1与公比q都不为零.⑥在数列{an}中每隔k(k∈N*)取出一项,按原来顺序排列,所得新数列仍为等比数列且公比为q^k+1数列{An}是等