堆排序原理_堆排序算法

经典算法--堆排序笔试题 - 其他综合 - 红黑联盟

957x622 - 123KB - JPEG

详解堆排序算法原理及Java版的代码实现 - PH

450x268 - 30KB - JPEG

数据结构 堆排序原理及其实现-C++-第七城市

220x167 - 16KB - JPEG

内部排序(3)选择排序 - 编程

2188x1722 - 900KB - JPEG

堆排序原理及算法实现(最大堆)

222x173 - 7KB - JPEG

常见排序算法的实现(归并排序、快速排序、堆

865x457 - 55KB - PNG

数据结构 堆排序原理及其实现-C++-第七城市

225x164 - 16KB - JPEG

堆排序与优先队列——算法导论(7)_「电脑玩

432x227 - 61KB - PNG

浅谈MySQL排序原理与案例分析_Mysql_脚本之

865x558 - 147KB - PNG

算法分析(一)堆排序原理及java实现_「电脑玩物

409x166 - 31KB - PNG

最常用的 8 个排序算法:从原理到改进,再到代码

307x272 - 7KB - JPEG

某里P7程序员,竟不知Nio、堆排序!网友疑问:怎

640x484 - 42KB - JPEG

最常用的 8 个排序算法:从原理到改进,再到代码

308x303 - 9KB - JPEG

排序技术_各种算法原理 图解 代码兑现_软件开

671x443 - 51KB - JPEG

浅谈MySQL排序原理与案例分析 - MySQL - 方

865x558 - 55KB - JPEG

简介：堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组

6 原理过程 如何建立这个堆呢。可以从空的堆开始,然后依次往堆中插入每一个元素,直 并不是将这些数完全用堆排序完成排序*/ 66 67 int i; 68 for(i = heapSize/2; i = 0; i--) 69 {

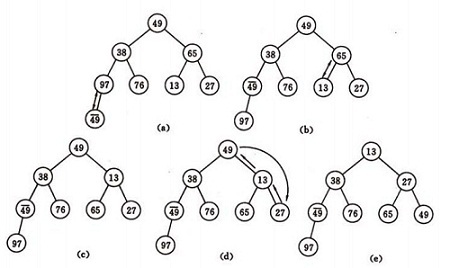
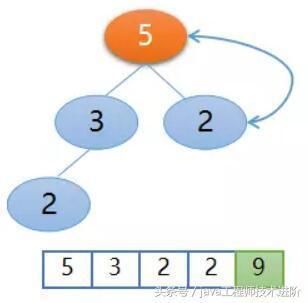
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构

堆排序算法的原理和实现 champion_. 堆排序算法的原理和实现 起源 1991年计算机先驱 堆排序的特点是:在排序过程中,将R[l.n]看成是一棵完全二叉树的顺序存储结构,利用完全

堆排序堆排序是利用堆的性质进行的一种选择排序。下面先讨论一下堆。 1.堆堆实际上是一棵完全二叉树,其任何一非叶节点满足性质: Key[i] =key[2i+1]&&Key[i] =key[2i+2]或者

那么树中任一非叶结点的关键字均不大于(或不小于)其左右孩子(若存在)结点的关键字,堆排序的时间复杂度为O(N*logN),这里我们就来详解堆排序算

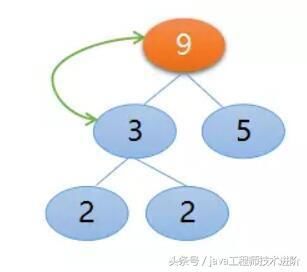
如果是最大堆,那么堆顶元素就是最大的。并且它是一种二叉树的形式。因此它的左右子树也是一个最大堆。也就说左子树和右子树的根都是当前子树中最大的元素。堆排序的原理就是维护一个最大堆。可以详见数据结构书,那段代码写的相当简洁易懂。初始化堆时,要弄明白为什么是更新一半的元素。你可以在纸上画一画,对每一个元素从二叉树上从1开始标号。会发现标号为1 , 2,..n/2 的结点刚好可以覆盖二叉树的所有路径,并且是从 n/2 到 1 去更新堆,这样的话就可以构成一个初始化的最大堆。每次更新最大堆时,都是沿着左右子树的路径一次更新,要左右子结点较大的元素往上移动,知道更新的元素大于左右子树的结点值。那么就成了一个新的最大堆。复杂度就是二叉树数的层数。即每次更新复杂度是log(n).

#include <stdio.h> void swap(int* a, int* b) { int t; t = *a; *a = *b; *b = t; } void maxHeapify(int* a, int i, int n) { int l, r, m; do{ r = (i+1) << 1; l = r - 1; m = l < n && a[l] > a[i] ? l : i; m = r < n && a[r] > a[m] ? r : m; if(i != m) swap(a+i, a+m), i = m; else break; }while(1); } void heapSort(int* a, int n){ int i; for(i = (n-1)/2; i >= 0; --i) maxHeapify(a, i, n); for(i = n-1; i > 0; --i) { swap(a, a+i); maxHeapify(a, 0, --n); } } void p

与内存管理中提到的“堆”是两个不同的概念,后者堆内存类似链表的数据结构。下面首先介绍堆数据结构特性,然后将如何建立最大堆或最小堆,最后再讲解堆排序原理及其实现