时间复杂度nlogn_时间复杂度o nlogn

算法时间复杂度的表示法O(n)、O(n)、O(1)、O

600x334 - 68KB - JPEG

时间复杂度 nlogn - 蓝讯

280x220 - 76KB - PNG

大O算法复杂度表示 - 综合编程类其他综合 - 红

652x378 - 22KB - JPEG

下列排序算法中,哪些时间复杂度不会超过nlog

818x860 - 145KB - PNG

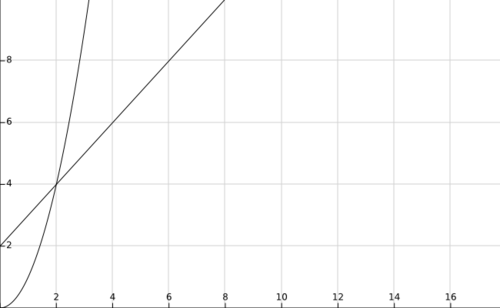
如何理解算法时间复杂度的表示法O(n)、O(n)、

500x308 - 15KB - JPEG

时间复杂度 nlogn - 蓝讯

280x220 - 19KB - PNG

PHP算法大全(1)基础篇-时间复杂度和空间复杂

603x261 - 21KB - JPEG

几种常见排序算法的Java实现及时间复杂度_J

638x294 - 40KB - PNG

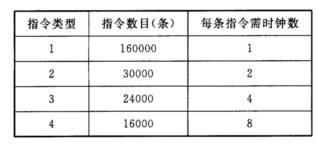
下列排序算法中,时间复杂度为O(nlogn)且占用额

335x145 - 12KB - JPEG

设n为整数,指出下列各算法的时间复杂度。_考

486x417 - 19KB - JPEG

数据结构中的时间复杂度与空间复杂度的求法

605x516 - 187KB - PNG

算法的时间复杂度_PHP教程_第七城市

1023x610 - 48KB - PNG

算法的时间复杂度_PHP教程_第七城市

1021x606 - 18KB - PNG

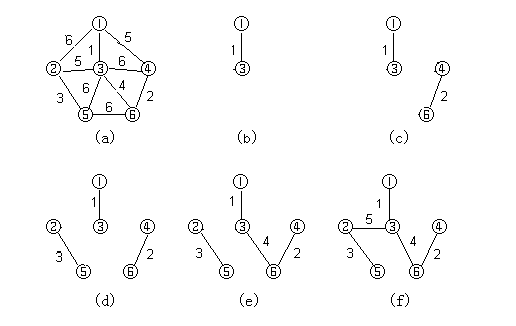
克鲁斯卡尔算法的时间复杂度为多少

516x326 - 2KB - PNG

最详细的算法解说-时间和空间复杂度

595x385 - 14KB - JPEG

本文以快速排序为例,推导了快排的时间复杂度nlogn是如何得来的,其它算法与其类似。对数据Data = { x1, x2. xn }: T(n)是QuickSort(n)消耗的时间; P(n)是Partition(n)消耗的时间;

归并排序算法复杂度为nlogn,算法是先分后并 用递归来分,每次分二分之一(该部分时间复杂度logn) 合并的时候两数组依次比较加入新数组中(该部分时间复杂度为n) #include ios

时间复杂度这个东西,其实更准确点说应该是描述一个算法在问题规模不断增大时对应的时 间增长曲线。所以,这些增长数量级并不是一个准确的性能评价,可以理解为一个近似

快速排序的时间复杂度为O(nlogn),最坏时间复杂度为O(n^2),最坏的情况适之每次区间划分的结果都是基准关键字的最左边或者右边,即选择的数字是待排序列中最小或者最大的

在描述算法复杂度时,经常用到o(1), o(n), o(logn), o(nlogn)来表示对应算法的时间复杂度。这里进行归纳一下它们代表的含义:这是算法的时空复杂度的表示。不仅仅用于表示时间

今天才搞清楚排序算法的O(N*logN)是什么意思 算法复杂度中的O(logN)底数是多少 最长递增子序列 O nlgn时间复杂度 快速排序的时间复杂度nlogn是如何推导的? O(nlogn)求逆

因为在顺序表中删除和插入的时间复杂度是n 8 tmp = arr.splice(i,1)[0]; 9 arr.splice(j,0,tmp); 10 } 11 }else if(arr[i] arr[j] && arr[i] = arr[j - 1]){ 12 tmp = arr.splice(i,1)[0]; 13 arr.splice(j

以2为底,ln以e为底。在算时间复杂度的时候,大O会忽略其中的常数项已经低阶项,所以你的公式应该写成O(logn) 回复于: 2012-01-13 10:05:59 #3得分:0 对我有用[0]丢个板砖[0

快速排序的平均时间复杂度就是O(NlogN):#include<stdio.h> #define N 5 int partition(int *a,int left, int right){ int leftptr,rightptr,pivot,t; pivot=a[right]; leftptr=left-1; rightptr=right; while(1){ while(a[++leftptr]<pivot); while(right>0&&a[--rightptr]>pivot); if(leftptr>=rightptr) break; else t=a[leftptr],a[leftptr]=a[rightptr],a[rightptr]=t; } t=a[leftptr],a[leftptr]=a[right],a[right]=t; return leftptr; } void quicksort(int *a,int left, int right){ int m; if(right-left<=0) retu

LCS(Longest Common Subsequences)最长公共子序列用一般的动态规划时间复杂度O(N^2),但经过优化可以达到O(NlogN),下面是转载集训队某人的最长递增子序列解题报告。