直线积分路径_ps路径曲线变直线

从原点到点 1 i的直线段;(2)抛物线 y x 2上从原点到点 1 i的弧段;(3)从原点沿 x轴到点 1再到 1 i的折线.解 (1)积分路径的参数方程为 y z ( t ) t it (0 t 1), i 1 i于是 Re z t , dz (1 i )dt , 1

复变函数中,积分路径C是i到2+i的直线段,则C的参数方程是Z=(1-t)i+t(2+i),为什么,怎么解的 下载作业帮 扫二维码下载作业帮 4亿+用户的选择 下载作业帮安装包 扫二维码下载作

计算其积分路径为沿不与直线y=x相交的路径． 找答案首页大学专科公共基础高等数学类问题详情 计算其积分路径为沿不与直线y=x相交的路径． 悬赏：0答案豆 提问人：匿

f(1-z)dz,其中积分路径C为从点0到点1+i的直线段 (此问题共3人浏览过)我要回答: f(1-z)dz,其中积分路径C为从点0到点1+i的直线段(图2)===以下答案可供参考=== 供参考答案1

f(1-z)dz,其中积分路径C为从点0到点1+i的直线段 f(1-z)dz,其中积分路径C为从点0到点1+i的直线段 在线等求速度. 在线等求速度 展开 Kuroro丶库洛洛 2014-01-15 Kuroro丶库

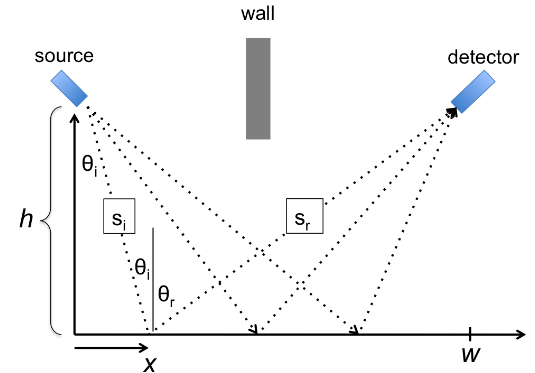
我们可以比较容易的计算出始末点不再以 f r rq2为中心的放射状电场的一条直线上的积分 ∫ E.ds 。我们的方法是 i选择一个如下图所示的直线积分路径。注意从 o点到 f点的积

简介：对于密度不均匀的物件，就需要用到曲线积分,dm=ρ(x,y)ds;所以m=∫ρ(x,y)ds;L是积分路径，∫ρ(x,y)ds就叫做

设z=a+jb,代入即可

积分与路径无关就是积分只要考虑起点与终点即可,中间不管它是什么路径。而不是说它的积分是恒等于0的。 因此我们真正在算积分时往往是找好算的路径,比如是直线情况。

与路径无关和直不直线没关系,只是路径无关之后我们用直线路径好算而已。积分路径是直线就是直线呗,直接算就是呗

线积分与路径无关性.pdf

800x1132 - 153KB - PNG

10-2第二类曲线积分.ppt

960x720 - 60KB - JPEG

设f(x)二阶连续可导,且曲线积分∫[3f(x)一2f(x)+

473x357 - 72KB - JPEG

线面积分典型例题.doc

993x1404 - 76KB - PNG

曲线曲面积分竞赛题整理.doc

993x1404 - 95KB - PNG

7年高中数学 第一章 导数及其应用 1.7 定积分的

141x200 - 10KB - PNG

74LS00 - 知乎

535x373 - 23KB - PNG

剖析上海交通大学复变函数复习习题.doc

993x1404 - 68KB - PNG

种种因素分析法的局限性及若干改进想法 - 全刊

247x360 - 17KB - JPEG

高斯公式和斯托克斯公式课件.ppt

1152x864 - 360KB - PNG

大学教授用甄嬛体教高数,同学大呼:老师太可

550x413 - 49KB - JPEG

矢量场的旋度讲述.ppt

960x720 - 96KB - JPEG

矢量场的旋度讲述.ppt

141x200 - 6KB - JPEG

同步辐射历史及现状

574x421 - 34KB - JPEG

教授甄嬛体教高数!同学大呼:老师太可爱了!

597x448 - 28KB - JPEG