对于满足一些条件的曲线,起点和终点的位置固定,沿不同的路线积分,其积分值相同,即曲线积分只与起点和终点有关,与路线的选取无关。 中文名 曲线积分与路径的无关性 应用
1;格林公式的条件是:闭区域D由分段光滑曲线L围成,函数P(x,y)及Q(x,y)在D上有一阶连续偏导数. 2;曲线积分与路径无关的充要条件是:区域D是一个单连通域,函数P(x,y)及Q(x,y)在
第八章第四节平面曲线积分与路径无关的条件一、平面上曲线积分与路径无关的条件一、平面上曲线积分与路径无关的条件定理8-4.设D是单连通域函数在D内具有一阶连续偏
一、格林公式二、平面上曲线积分与路径无关的条件三、二元函数的全微分求积§10.3格林公式及其应用上页下页铃结束返回首页一、格林公式v单连通与复连通区域 v区域的
平面上曲线积分与路径无关的条件是什么 作业帮用户2016-12-11 扫二维码下载作业帮 4亿+用户的选择 一个在任何条件下适用的条件是原函数存在. 如果积分区域是单连通区
一、格林公式二、平面上曲线积分与路径无关的条件三、二元函数的全微分求积 §10.3格林公式及其应用上页下页铃结束返回首页海拓凸瞄帧蛾驳粒槐季寡力剔痊瞳炽摇顺肇
第三节一、格林公式二、积分与路径无关的条件格林公式及其应用第十一章三、原函数四、全微分方程区域D分类单连通区域(定理1.设区域D是由分段光滑曲线L围成,则有 Gre
无旋场的路径积分才能是0,证明方法是先对简单区域证明,然后对复杂区域进行分解,归纳为简单区域。2维向量场旋度的定义是qx-py。
一是求原函数:arctan(y/(2x))是原函数。注意到原函数在x=0的地方不可微,因此 积分时的上下限就要以之为分界点。比如本题,在y轴上去点 E(0,-1),F(0,1)。则 先计算从A到E的积分值是lim arctan(y/(2x))-arctan(0/(2*-1)) =pi/2。注意,此式取极限时要求y趋于-1,x从小于0的地方趋于0, 因此y/(2x)是趋于正无穷,极限是pi/2。 再计算从E到F的积分,取极限是也要注意正负号, 在E点时y趋于-1,x从大于0的方向趋于0,因此极限是-pi/2, F点y趋于1,x从大于0的方向趋于0,极限是pi/2,两者相减是pi。 再从F到D类似计算可得结果。 另外做法与之类似。 先计算绕一圈AEBFA(L)的积分。这个可以用挖洞的Green公式。 以原点为心做一个小椭圆S:4x^2+y^2=e^2,e充分小,方向为逆时针。 则L的积分-S的积分=0(这是Green公式), 因此L的积分=S的积分 =S上(xdy-ydx)/(e^2) 再用Green公式 =2S包围的面积/e^2 =pi。(好像是这个结果,你再仔细计算吧) 于是ABD的积分+DA的积分=pi, 计算出DA的积分即可
就是沿不同路径进行积分,结果都是一样,它有个等价说法,就是环路积分为0.举个例子,物理里的重力,势能du=-引力F向量.dr向量,重力势能从A点到B点,不论你过程中经过什么路径,最终的势能变化都是Ub-Ua。因此从物理的角度,曲线积分与路径无关就是势。 从数学的角度来看,满足这个条件的线积分,其微分项,能够组成一个全微分,比如ydx+xdy=d(xy).

曲线积分与路径无关的条件PPT_word文档在线
1080x810 - 77KB - JPEG

曲线积分和路径无关的条件.ppt
141x200 - 2KB - JPEG

格林公式_曲线积分和路径无关的条件ppt.ppt
141x200 - 3KB - JPEG
![曲线积分与路径无关的条件[精选].ppt](http://txt25-2.book118.com/2017/0125/book86649/86648380_small.jpg)
曲线积分与路径无关的条件[精选].ppt
141x200 - 5KB - JPEG

与路径无关的定义曲线积分与路径无关的条件二
800x600 - 222KB - PNG

5.3.2 平面曲线积分与路径无关的条件;4.3.3(1)
1080x810 - 91KB - JPEG

第三节格林公式及曲线积分与路径无关的等价条
1152x864 - 157KB - PNG

平面曲线积分与路径无关的条件_中华文本库
892x739 - 553KB - PNG

平面曲线积分与路径无关的条件_中华文本库
892x843 - 743KB - PNG

平面曲线积分与路径无关的条件_中华文本库
892x892 - 733KB - PNG
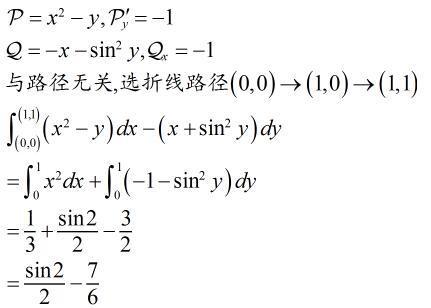
应用积分与路径无关的条件,∫L(x-y)dx-(x+siny)
431x308 - 15KB - JPEG

第四节 平面上曲线积分与路径无关的条件
1080x810 - 55KB - JPEG

线积分与路径无关性.pdf
800x1132 - 153KB - PNG

格林公式、曲线积分与路径无关的条件ppt
1080x810 - 52KB - JPEG

10-6 平面曲线积分与路线无关的条件.ppt
960x720 - 1059KB - PNG