像Tu中那样把极坐标和直角坐标作个类比,能看出来Zhi角坐标中的曲线积分之所以不能 为什么证明极坐标面积公式和弧长公式不太统一如ds=0.5p^2da而不是ds=0.5*p*弧长微
首先求教一点---极坐标中长度关于角度的积分是不是弧长?如果是这一点,请帮我看看我 曲线y从a到b的弧长公式s=∫(a,b)√(1加y'^2)dx 追问: 我研究过这种积分方法,但有个问
像图中那样把极坐标和直角坐标作个类比,能看出来直角坐标中的曲线积分之所以不能直 公式把此方程化为直角坐标方程2016-12-16 扫描下载二维码 ©2019 作业帮联系方式
积分公式向左转|向右转
定积分的应用就是采用微元法,而微元法有个前提就是可以近似代换,教材弧长公式的推导思想是利用一段弧无穷小可以近似为直线了,而你却把每段弧近似为圆弧而微元积分这样
弧长公式 hse11111223|2018-06-29 |举报 专业文档 专业文档是百度文库认证用户/机构 非会员用户需要消耗下载券/积分获取。只要带有以下“VIP免费文档”标识的文档便是
1.平面曲线由直角坐标方程y=f(x)给出,曲线弧的端点A、B对应于自变量x的值分别为a、b(a<b),则平面曲线的弧长公式为 l=∫(a下b上)√1+[f'(x)] ² .dx. (√根号下的 .) 2.平面曲线由参数坐标方程x=φ(t),y=ψ(t)给出,曲线弧的端点A、B对应于参数t的值分别为α、β(α<β),则平面曲线的弧长公式为 l=∫(α下β上)√[φ'(t)]²+[ψ'(t)] ² .dt. 3.平面曲线由极坐标方程r=r(θ)给出,曲线弧的端点A、B对应于极角θ的值分别为α、β(α<β),则平面曲线的弧长公式为 l=∫(α下β上)√[r(θ)]²+[r'(θ)]² .dθ.
关于极坐标弧长公式.极坐标弧长公式书上写的是将ρ=rθ转为x y的参数方程,微分式为 当曲线是圆的时候可以用这个公式来积分从0到2π因为圆的每一段弧都是光滑的但是曲
√[(dx)^2+(dy)^2],当曲线方程是直角坐标方程、参数方程、极坐标方程时,ds有不同的表达式,根据这些不同的表达式,确定出相应的积分上下限即可. 当曲线方程是参
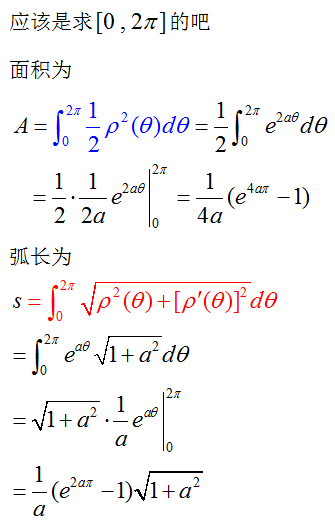
求对数螺线的弧长公式和面积公式。面积公式很
335x523 - 8KB - PNG

圆的极坐标方程公式 简单曲线极坐标方程公式
468x292 - 26KB - JPEG

【复旦高数学习周刊】第二期丨愚人节,大神如
600x421 - 30KB - JPEG

大学高等数学_17对弧长和曲线积分_对坐标曲
1080x810 - 80KB - JPEG

1对弧长的曲线积分2对坐标的曲线积分3对面积
960x720 - 57KB - JPEG
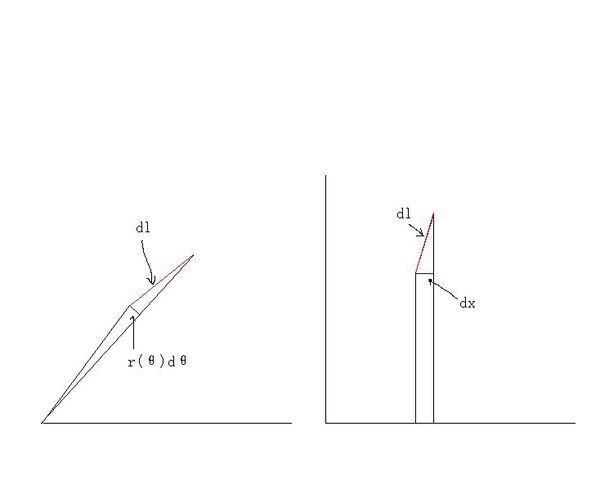
极坐标方程的弧长公式是怎么证明哒?
600x494 - 8KB - JPEG

第19讲-对弧长曲线积分.doc
993x1404 - 73KB - PNG

D111 对弧长的曲线积分.doc
870x1229 - 68KB - PNG

第6章定积分的应用分析.ppt
960x720 - 28KB - JPEG

Ch4.2-第一类曲面积分.ppt
1200x900 - 55KB - PNG

《一元积分学的几何应用与重积分计算.doc
141x200 - 17KB - PNG
![[精品文档]一元积分学的几何应用与重积分计算](https://txt39-2.book118.com/2018/0611/book172070/172069148.png)
[精品文档]一元积分学的几何应用与重积分计算
993x1404 - 121KB - PNG

第10章定积分的应用 (二).ppt
1152x864 - 523KB - PNG

9-1二重积分的概念与性质讲述.ppt
960x720 - 169KB - PNG

高等数学下册高等职业教育十一五规划教材通
141x200 - 5KB - JPEG