基础解系的求法_基础解系的求法例题及其通解算法

4.3 齐次线性方程组解的构造.pptx

1152x864 - 95KB - PNG

线性代数---第四章 线性方程组 4.2 齐次线性方

800x600 - 355KB - PNG

4–5线性方程组的解的结构.pptx

141x200 - 5KB - JPEG

齐次线性方程组有非零解的条件及解的结构.pp

141x200 - 5KB - JPEG

线性代数(苏州大学)电子教案 xxds-ch5-5.ppt

1152x864 - 799KB - PNG

线性代数课件xxds10章节.ppt

1152x864 - 249KB - PNG

51矩阵的特征值及特征向量.ppt

141x200 - 5KB - JPEG

微博 文章 - 2016考研数学线性方程组解的判别

574x750 - 135KB - JPEG

大学数学系列辅导讲座.ppt

1152x864 - 211KB - PNG

矩阵Jordan标准形及过渡矩阵的同步求解问题.

993x1404 - 80KB - PNG

矩阵的相似变换.ppt

1152x864 - 523KB - PNG

2015考研数学二解析:特征值与特征向量

550x384 - 21KB - JPEG

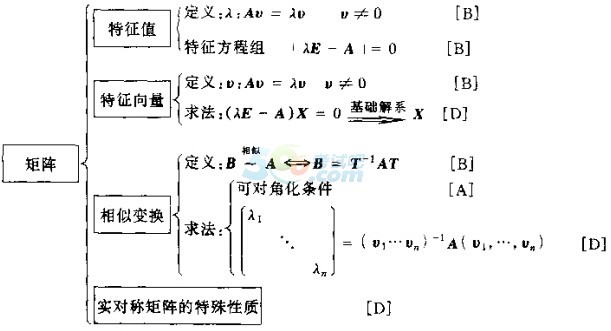
2015考研数学知识框架图:矩阵特征值和特征向

611x331 - 38KB - JPEG

2016考研线性代数重难点解析--基础解系

600x635 - 237KB - PNG

线代里的小疑问如图,这两个基础解系是不是一

576x1024 - 45KB - JPEG

求基础解系的方法书上做法：确定主元为x1x3x4后，自由未知量x2x5取（1，0）（0，1），?“主元为x1x3x4后，

内容提示：矩阵中的基础解系解法-PPT（精） 文档格式：PPT|浏览次数：5811|上传日期：2015-05-14 13:06:48|

也可以看秩为几,则基础解析的个数边为行列式阶数减去秩的个数；二、换另外一支笔,把主对角线上的零元素都改

如图，从矩阵中怎么算出下面的基础展开全部 求“基础解系”，需要将带求矩阵变为“阶梯形矩阵”（变换方法

求解答 特征向量的.画框部分是怎么求出来的呐？那它基础解系求法是一样的吗？自由变量为什么可以随便取数

解系求法举例 求齐次线性方程组 的一个基础解系和通解 解:将增广矩阵变为上阶梯形(用初等行变换)原方程组同

如何求解线性代数的基础解系？请展开全部 就以齐次方程组为例： 假如是3阶矩阵 r(A)=1 矩阵变换之后不就是