
浅谈多元函数连续附可微转载.doc
993x1404 - 61KB - PNG

高等数学,多元函数。z=|x-y|为什么在x=0,y=0处
600x363 - 40KB - JPEG
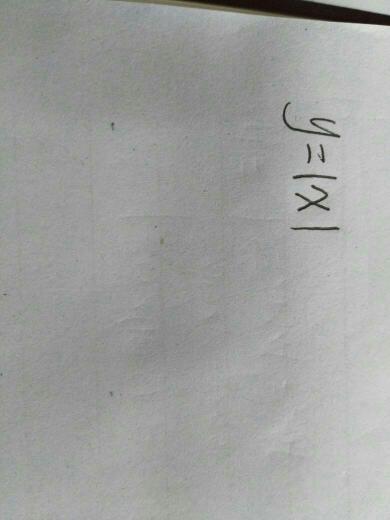
为什么多元函数连续不能证明可导?
390x520 - 16KB - JPEG

2018考研数学重点:多元函数微分学精析
607x636 - 361KB - JPEG

多元函数微分法习题课#.ppt
141x200 - 5KB - JPEG

2018考研数学重点:多元函数微分学精析
625x633 - 68KB - JPEG

2018考研数学重点:多元函数微分学精析
607x636 - 63KB - JPEG

多元函数中的疑问,11.5.5证明里最后一行打问号
375x500 - 209KB - JPEG

高等数学多元函数证明题
433x239 - 12KB - PNG

多元函数的极限连续性-已技巧.ppt
960x720 - 71KB - JPEG

关于多元函数的偏导数与全微分的题_360问答
600x479 - 356KB - PNG

多元函数微积分第一章.doc
141x200 - 8KB - PNG

高等数学课件d81多元函数的基本概念.ppt
1152x864 - 742KB - PNG

多元函数的极限与连续习题.doc全文-规范文件
993x1404 - 58KB - PNG

八节多元函数极值及其求法.doc
993x1404 - 87KB - PNG
天杨说的很对,但是证明二元函数可微没有充分必要条件,我给的就是个充分条件,可以用这个思路去证明可微性
对于一元函数,可微性比较容易判定。因为一元函数在某个点连续、可导、可微这三个概念的关系是很清楚的,可
如何判定二元函数的可微性 456bxq|2014-05-11|暂无评价|0|0|专业文档 专业文档是百度文库认证用户/
证明函数连续,连续的条件是“左极限=右极限”,且在左右极限连接点有定义,且其值多元函数:偏导存在且连续
y=f(x),在x点可微,只要证明下面的对于二元以及多元的函数来说,一般不说函数可微吧(我是大二,非数学专业
证明多元函数可微主要有两种方法:方法一:证明偏导存在且连续方法二 用定义.简单来说就是全增量的表达式和
请问如何不用证明就知 说明一个命题不正确是不需要证明的,只需举一个反例即可,因为存在函数可微而偏导数不
二元函数可微的定义是函数z=f(x,y)在点(x,y)的全增量Δz=f(x+Δx,y+Δy)-f(x,y)可以表示成Δz=AΔx+BΔy+o
如图,如何证明多元函数如果不可微,则一阶偏导数一定不连续这个命题!可以用逆否命题证明,可是它的本质是