 微分中值定理的进一步探讨
微分中值定理的进一步探讨
1461x2096 - 997KB - PNG
 积分第二中值定理的证明.doc
积分第二中值定理的证明.doc
993x1404 - 77KB - PNG
 第章微分中值定理及其应用().doc
第章微分中值定理及其应用().doc
993x1404 - 103KB - PNG
 Chapter05.1-3微分中值定理、洛必达、
Chapter05.1-3微分中值定理、洛必达、
1080x810 - 41KB - JPEG
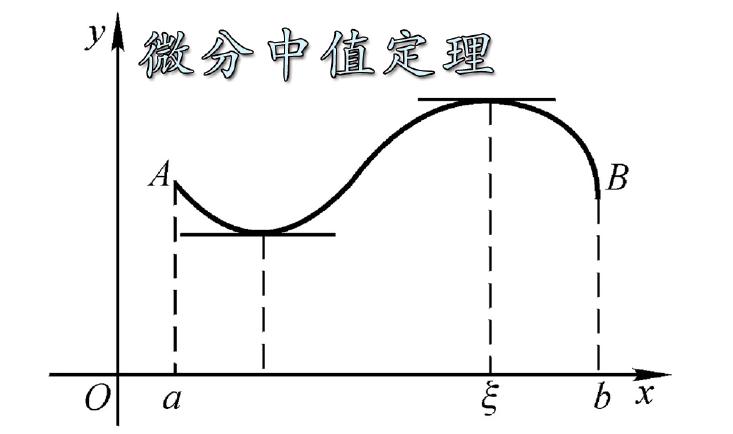 微分中值定理的应用
微分中值定理的应用
733x434 - 47KB - JPEG
 泰勒中值定理1
泰勒中值定理1
1080x810 - 141KB - JPEG
 2-6.中值定理ppt
2-6.中值定理ppt
1080x810 - 74KB - JPEG
罗尔中值定理
1080x810 - 74KB - JPEG
 罗尔中值定理的推广
罗尔中值定理的推广
1430x2053 - 1088KB - PNG
罗尔中值定理
1080x810 - 79KB - JPEG
罗尔中值定理
1080x810 - 137KB - JPEG

857x857 - 58KB - JPEG
 微分中值定理
微分中值定理
695x517 - 400KB - PNG
积分中值定理
1080x810 - 318KB - JPEG

416x416 - 12KB - JPEG
简介:拉格朗日中值定理又称拉氏定理,是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形。定理拉格朗日中值定